Exponentialfunktionen der Form $$y=a*b^x$$

Erinnerst du dich, dass du Parabeln strecken und stauchen kannst?

Das geht auch mit Exponentialfunktionen. In der Funktionsgleichung wird ein Parameter $$a$$ hinzugefügt:
$$y=a*b^x$$.

Die Eigenschaften der Funktion verändern sich dann.

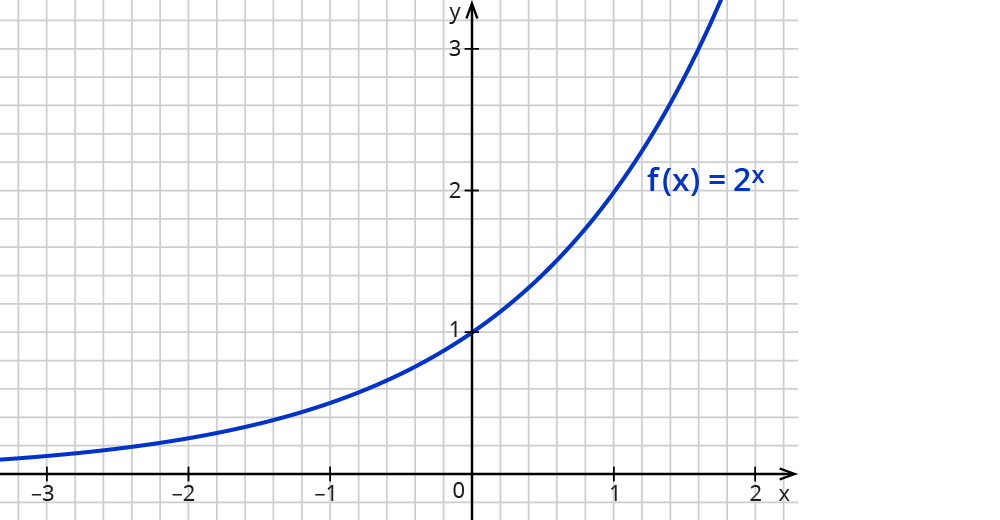
Betrachte zunächst wieder ein Beispiel: $$y=3*2^x$$ und im Vergleich dazu nochmals die Funktion $$y=2^x$$.

Die Exponentialfunktionen $$y=2^x$$ und $$y=3*2^x$$

Sieh dir die Wertetabelle an:

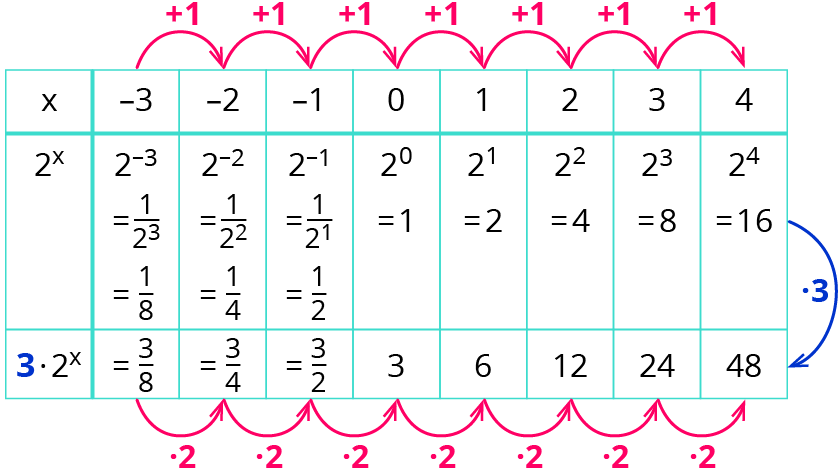
Wie du siehst, verdoppeln sich bei beiden Funktionen die y-Werte in jedem Schritt. Der Faktor $$3$$ bewirkt, dass jeder y-Wert von $$3*2^x$$ das Dreifache von $$2^x $$ ist.

Für das Berechnen der y-Werte sind die Potenzgesetze hilfreich:

Für Potenzen $$a^b$$ mit $$a \in \mathbb{R}$$ und $$b \in \mathbb{Z}$$ gilt:
$$a^-b=1/{a^b}$$ und $$a^0=1$$.

Die Graphen von $$y=2^x$$ und $$y=3*2^x$$

Betrachte nun die Graphen beider Funktionen.

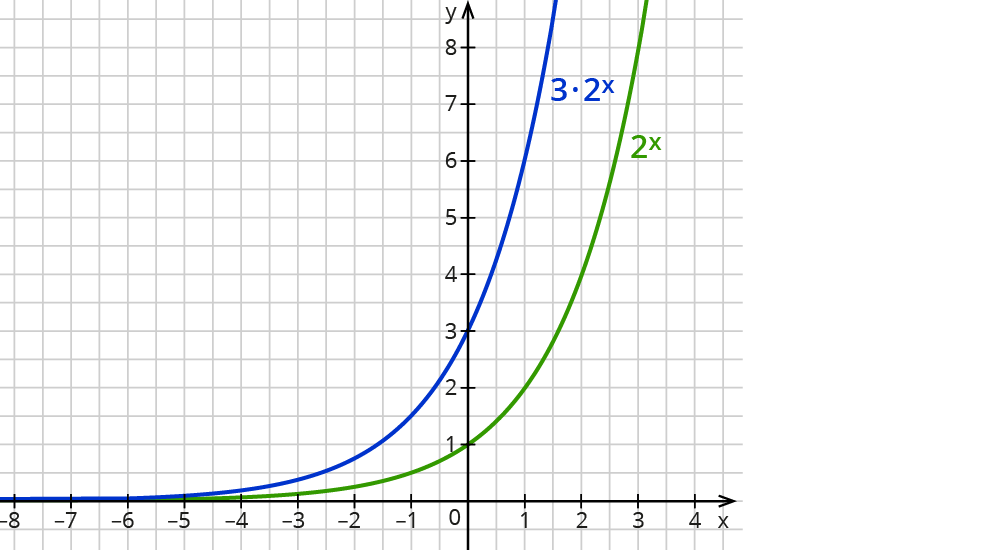
Wie du erkennen kannst, bewirkt der Faktor 3 eine Streckung des Graphen in y-Richtung um den Faktor 3.

Definition: Exponentialfunktionen der Form $$y=a*b^x$$

Eine Funktion mit der Gleichung $$y=a*b^x$$ mit $$a ne 0$$, $$b>0$$ und $$b ne 1$$ heißt Exponentialfunktion zur Basis $$b$$ mit dem Streckfaktor $$a$$.

Das $$b$$ heißt Wachstums- bzw. Zerfallsfaktor.

Das $$a$$ kann als Startwert bei exponentiellen Wachstums- bzw. Zerfallsvorgängen aufgefasst werden. Dazu später mehr.

Graphen von $$y=a*2^x$$

Hier siehst du verschiedene Funktionen der Form $$y=a*2^x$$ mit verschiedenen Werten für $$a$$.

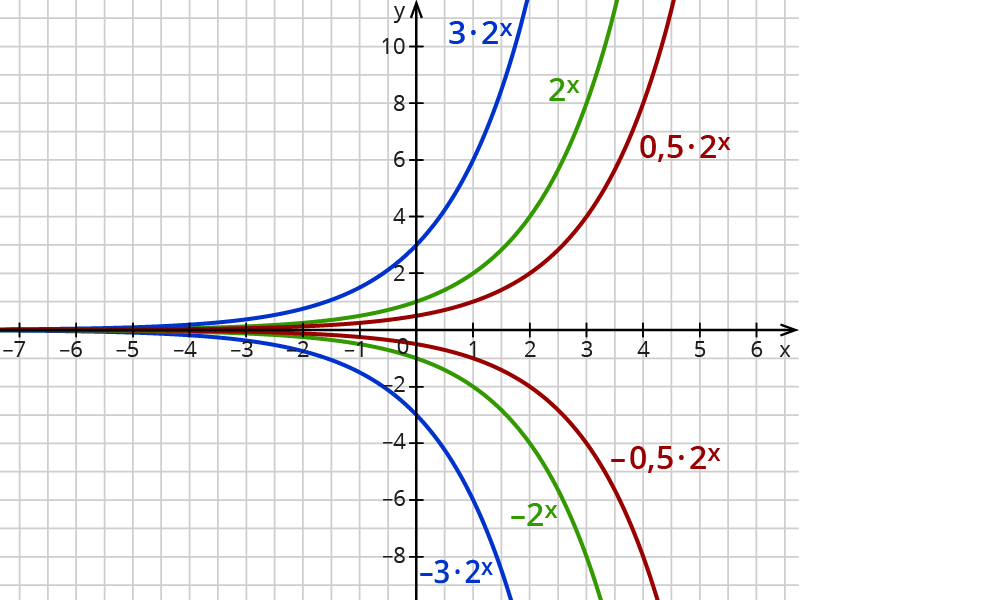
Siehst du die Zusammenhänge zwischen den Graphen?

• Der Graph fällt für $$b$$ zwischen $$0$$ und $$1$$ (exponentieller Zerfall).
  Der Graph steigt für $$b$$ größer $$1$$ (exponentielles Wachstum).

• Der Faktor $$a$$ bewirkt eine Streckung in y-Richtung, falls $$a>1$$ (z.B. $$3$$; $$5,5$$; $$20$$). Das ist auch so, wenn $$a<-1$$ ist (z.B. $$-3$$; $$-5,5$$; $$-20$$).

• Der Faktor $$a$$ bewirkt eine Stauchung in y-Richtung, falls er zwischen $$0$$ und $$1$$ liegt. (z.B. $$0,5$$)

• Das ist auch so, wenn $$a$$ zwischen $$-1$$ und $$0$$ liegt. (z.B. $$-0,5$$)

• Die Graphen der Funktionen $$y=a*b^x$$ und $$y=-a*b^x$$ sind Spiegelbilder. Die Spiegelachse ist die x-Achse.

• Die Graphen liegen alle oberhalb der x-Achse, solange $$a>0$$ ist.

• Für $$a=1$$ hat die Funktion die Form $$y=b^x$$.

• Die Graphen schmiegen sich der x-Achse an.

• Alle Graphen verlaufen jetzt durch den Punkt $$P(0|a)$$, nicht mehr durch $$Q(0|1)$$.

Bestimmen von Funktionsgleichungen der Form $$y=a*b^x$$ aus zwei Punkten

Sicherlich erinnerst du dich daran, dass man bei Funktionsgleichungen der Form $$y=b^x$$ nur einen Punkt brauchte, um sie eindeutig zu bestimmen.
Da du es hier mit einem Parameter mehr zu tun hast, brauchst du zwei Punkte.

Aufgabe: Gib die Gleichung einer Exponentialfunktion an, deren Graph durch $$P(-2|0,16)$$ und $$Q(-1|0,8)$$ verläuft.

Ansatz:

$$y=a*b^x$$   | Punkte einsetzen

$$(I)$$ $$0,16=a*b^-2$$
$$(II)$$ $$0,8=a*b^-1$$   |$$:b^{-1}$$

$$(I)$$ $$0,16=a*b^-2$$
$$(II)$$ $$a=0,8/b^-1$$    |einsetzen in $$(I)$$

$$rarr$$ $$a$$ in $$(I)$$:
$$(I)$$ $$0,16=0,8/b^-1*b^-2$$

$$⇔ 0,16=0,8/b^2*b^1$$

$$⇔ 0,16=0,8/b$$

$$⇔ b=5$$

$$rarr$$ $$b$$ in $$(I)$$:
$$(I)$$ $$0,16=a*5^-2$$   |$$:5^-2$$

$$⇔0,16/5^-2=a$$

$$⇔ a= 4$$

$$⇒ y=4*5^x$$

Bestimmen von Funktionsgleichungen der Form $$y=a*b^x$$ aus Texten

Bei vielen Aufgaben erstellst du erst mal aus dem Text eine Funktionsgleichung. Mit der kannst du dann weiterrechnen.

$$a)$$ Veränderung pro 1 Zeiteinheit:

Beispiel:
Ein Anfangsbestand von 75 vervierfacht sich jede Stunde ($$x$$ →1 Stunde).
Dann ist $$a=75$$ (der Anfangsbestand) und $$b=4$$ (Wachstumsfaktor, Vervierfachung pro Stunde).

Also: $$y=75*4^x$$.

$$b)$$ Veränderung bei beliebiger Zeiteinheit

Beispiel:
Ein Anfangsbestand von 75 vervierfacht sich alle 3 Stunden (x → 1 Stunde). $$a$$ ist immer noch 75. Der Wachstumsfaktor muss sich nun aber verändern, weil eine Vervierfachung nun erst nach 3 Stunden erfolgt. So sieht das in der Wertetabelle aus:

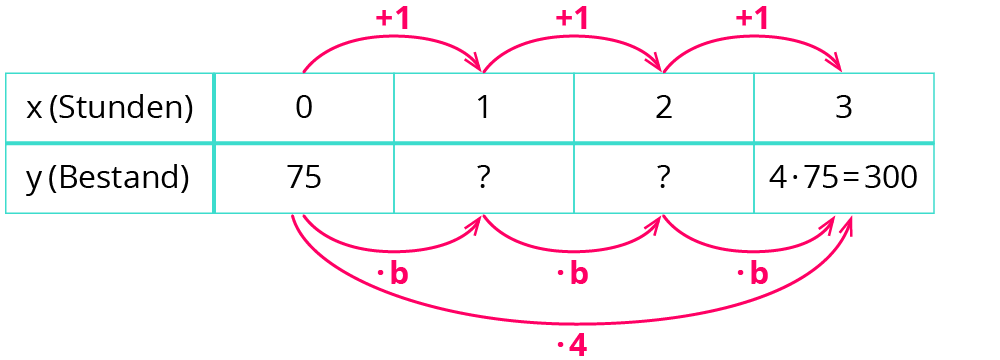
Die Pfeildarstellung entspricht der Gleichung

$$b*b*b=b^3=4$$   |3. Wurzel ziehen
$$⇔ b=root(3)4$$

$$⇒ y=75*$$ $$(root(3) 4)^x$$.

Tipp: Beachte die Sätze mit um und auf.

Beispiel:
Ein Anfangsbestand von 18 nimmt pro Stunde um 10 % ab. Das heißt, dass nach 1 Stunde noch 90 % da sind. Prozentangaben wandelst du in Dezimalzahlen um.
Also: $$y = 18 *0,9^x$$ .