Kegel – Eigenschaften und Berechnung des Oberflächeninhalts
Was ist ein Kegel?
Wie kannst du die Größe der Verpackung bestimmen?

Bild: Langner & Partner Werbeagentur GmbH
In der Mathematik ist die Verpackung ein Kegel. Er hat
- einen Kreis als Grundfläche,
- einen gewölbten Mantel
- und eine Spitze.
Die Körperhöhe h ist der Abstand der Spitze von der Grundfläche. Die Verbindungsstrecke vom Kreisrand zur Spitze heißt Mantellinie s.

Was ist die Oberfläche eines Kegels?
Wenn du den Kegel zu einem Netz aufklappst, kannst du die Flächen gut erkennen.
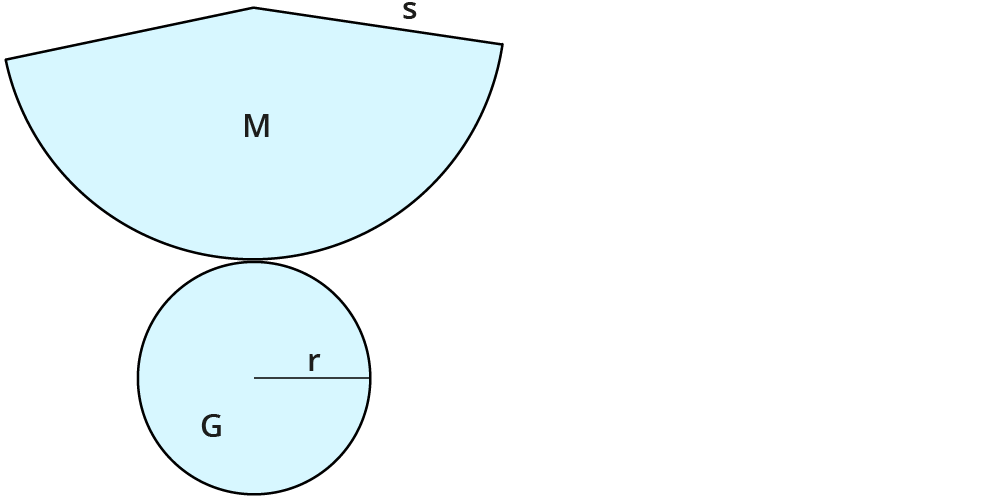
Die Oberfläche setzt sich aus der Grundfläche und der Mantelfläche zusammen.
Die Oberfläche ist die Fläche, die du berühren kannst, wenn du den Kegel in der Hand hältst.
So berechnest du die Mantelfläche
Die Grundfläche Kreis kannst du ja schon berechnen. Neu ist die Mantelfläche.
Zerlege den Mantel in Teile.
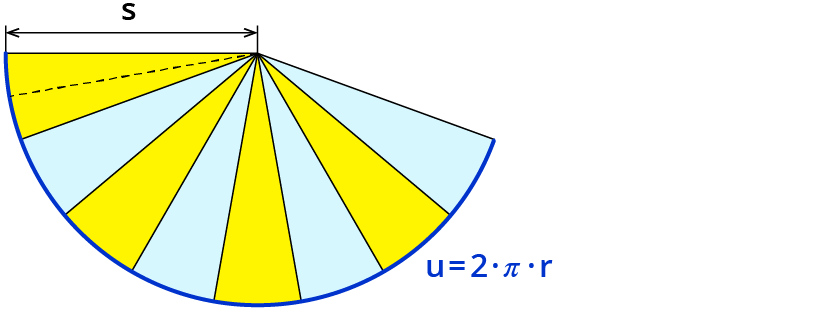
Lege die Teile in eine Reihe. Erinnert dich das an was?
Je feiner du die Teile wählst, desto mehr sieht die Figur
wie ein Rechteck aus.
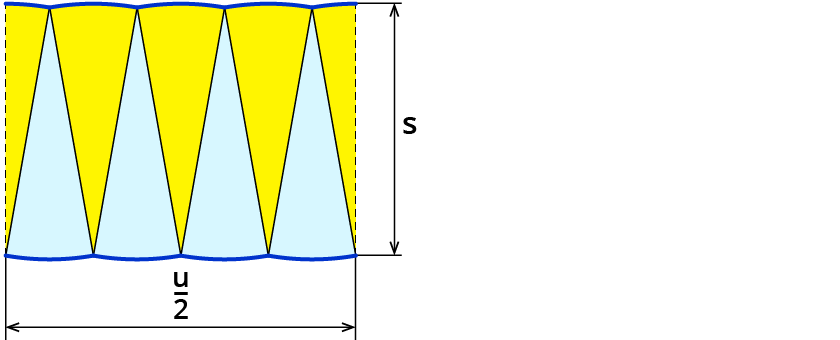
Den Flächeninhalt eines Rechtecks berechnest du mit a⋅b.
Also hier u2⋅s.
u2⋅s=2⋅π⋅r2⋅s=π⋅r⋅s
Die Mantelfläche berechnest du mit: M=π⋅r⋅s
Kreisformeln:
G=π⋅r2
u=2⋅π⋅r oder u=π⋅d

- r Radius
- d Durchmesser
- π Kreiszahl

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Die Formel für die Kegel-Oberfläche
Wie kommst du an die Mantellinie s?
Aus dem Radius r und der Kegelhöhe h kannst du mit dem Satz des Pythagoras die Mantellinie berechnen.

Benutze das rechtwinklige Dreieck mit den Seiten h, r und s .
Es gilt s2=r2+h2
Also s=√r2+h2
Dann ergibt sich für die Mantelfläche:
M=π⋅r⋅s
und damit: M=π⋅r⋅√r2+h2
So berechnest du den Oberflächeninhalt eines Kegels:
O=G+M
O=π⋅r2+π⋅r⋅s
O=π⋅r2+π⋅r⋅√r2+h2
So berechnest du die Oberfläche eines Kegels
Formel 1:
Gegeben ist ein Kegel mit r=8 cm und s=12 cm.
Um die Oberfläche des Kegels zu berechnen, gehe so vor:
O=π⋅r2+π⋅r⋅s
O=π⋅(8 cm)2+π⋅8 cm⋅12 cm
O=502,65 cm2
Formel 2:
Gegeben ist ein Kegel mit r=6 cm und h=15 cm.
Benutze die andere Formel, da h anstelle von s gegeben ist:
O=π⋅r2+π⋅r⋅√r2+h2
O=π⋅(6 cm)2+π⋅6 cm⋅√(6 cm)2+(15 cm)2
O=417,62 cm2
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen



