Lineare Funktionen beschreiben
Lineare Funktionen
Lineare Funktionen sind Zuordnungen.
Sie können unterschiedlich dargestellt werden:
- als Graph im Koordinatensystem
- in einer Tabelle
- als Funktionsgleichung in einem Funktionsterm
Lineare Funktionen gezeichnet
Lineare Funktionen kannst du als Geraden in ein Koordinatensystem zeichnen.
Hier siehst du die Graphen von drei verschiedenen linearen Funktionen:

Der Graph einer linearen Funktion ist immer eine Gerade.
Besonders einfach zu zeichnen!
Eine lineare Funktion kannst du also immer mit einem Lineal zeichnen.
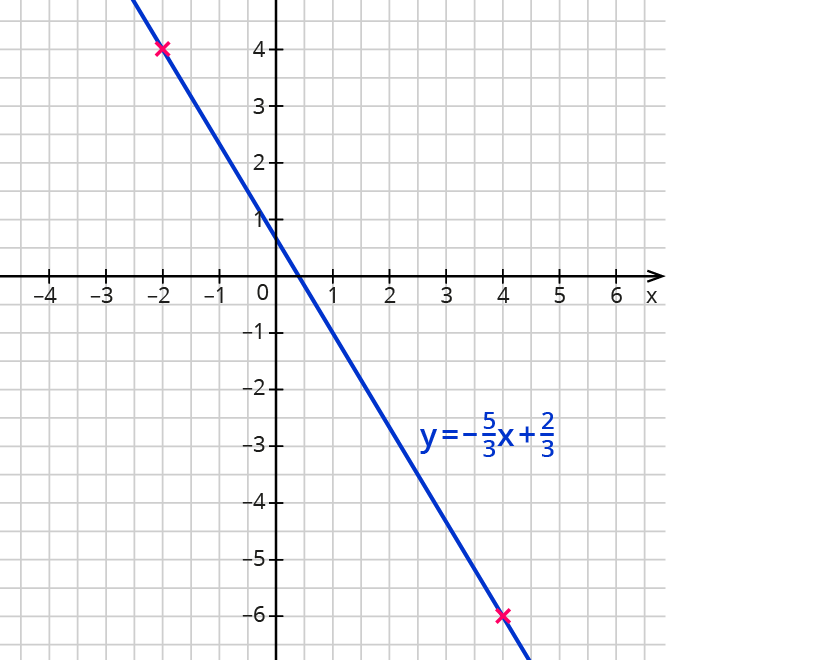
Hier siehst du den Graphen einer linearen Funktion, der durch die Punkte (-2∣4) und (4∣-6) festgelegt ist.

2 Punkte reichen, um eine lineare Funktion zu zeichnen.
Proportionale Zuordnungen – eine besondere Spezialität
Hier siehst du die Graphen von 3 besonderen linearen Funktionen.
Die Graphen gehen durch den Ursprung.
Zum Doppelten oder Dreifachen von x gehört auch das Doppelte oder Dreifache von y.
Sie heißen proportionale Funktionen.

Jede proportionale Funktion ist eine lineare Funktion.
Aber nicht jede lineare Funktion ist eine proportionale Funktion.
Teste hier dein Wissen zum Thema Proportionalität und Antiproportionalität mit vielen anschaulichen Übungsaufgaben!
Lineare Funktionen in einer Tabelle
In Tabellen erkennst du lineare Funktionen so:Wenn x immer um 1 zunimmt, dann ist die Veränderung des y-Werts jedes Mal gleich groß.

Änderung zwischen den x-Werten: immer +1
Änderung zwischen den y-Werten: immer -2
Ist die Änderung zwischen den x-Werten gleich, muss auch die Änderung zwischen den y-Werten gleich sein.
Erinnere: Eine Funktion ist eine Zuordnung, bei der jedem x-Wert genau ein y-Wert zugeordnet wird.
Lineare Funktionen als Terme
Der Funktionsterm für lineare Funktionen hat immer die Form m⋅x+b.
Die Funktionsgleichung ist y=f(x)=m⋅x+b.
Terme sind Rechenausdrücke. Ein Term heißt linear, wenn die Variable nur mit einer Zahl malgenommen wird.
Diese Zahl kann auch 0 oder 1 sein.
| Funktiongleichung | Lineare Funktion? |
|---|---|
| y=3x+4 | ja |
| y⋅x=4 | nein |
| y=4 | ja, denn y=0⋅x+4 |
| y=x | ja, denn y=1⋅x+0 |
| y=1x | nein |
| y=12⋅x+13 | ja |
| y=12+x2 | nein |
| y=x5+32 | ja, denn y=15⋅x+32 |
Definitions- und Wertebereich
Was genau versteht man eigentlich nochmal unter dem Definitions- und Wertebereich? Frische hier dein Wissen dazu auf.
Was sind nun Definitionsbereich D und Wertebereich W für lineare Funktionen?
D (alle x-Werte, die du in f einsetzen kannst): ℚ
W (alle y-Werte, die rauskommen können): ℚ
Manchmal siehst du auch andere Buchstaben im Funktionsterm: y=m⋅x+n
y=a⋅x+b
y=m⋅x+t
Dabei kannst du das Malzeichen hinschreiben oder weglassen!
nicht linear:

Ein Term ist nicht linear, wenn die Variable quadriert wird oder die Variable unten im Bruch – also im Nenner – steht.
ℚ sind die rationlen Zahlen
Lineare Funktionen in Worten
Mit linearen Funktionen können viele alltägliche Vorgänge beschrieben werden, bei denen von einem Anfangswert aus eine gleichmäßige Änderung (Zunahme oder Abnahme) stattfindet.
Beispiel:
Peter spart auf ein neues Fahrrad. 150 Euro hat er schon zusammen. Er nimmt sich vor, jeden Monat 5 Euro von seinem Taschengeld zu sparen.
Übersetze in eine Funktionsgleichung:
x: Anzahl der Monate
Peters angespartes Geld hängt von der Anzahl der Monate ab: y=f(x)=5⋅x+150
Anfangswert: 150
gleichmäßige Zunahme: 5⋅x
Warum? Der Sparbetrag wächst um 5 Euro pro Monat mal Anzahl x der Monate.
1 Monat später hat er 5 Euro mehr.
Funktionen zum Anfassen
Puh, war das alles ziemlich theoretisch?? So kannst du dir eine Funktion praktisch vorstellen:
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen