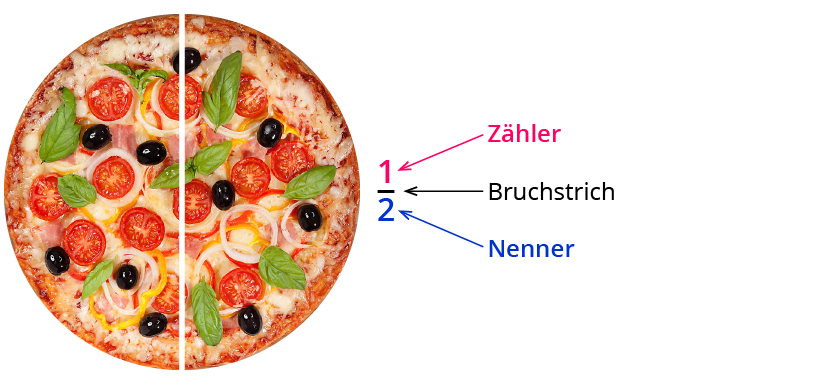
Natürliche Zahlen und Bruchzahlen vergleichen
Die Menge der Natürlichen Zahlen
Wenn du an Natürliche Zahlen denkst, dann kommen dir bestimmt eine ganze Reihe von unterschiedlichsten Zahlen in den Kopf, zum Beispiel
1, 3, 7, 25, 673, 2783 oder auch ganz große Zahlen wie 2.364.708 (Zweimillionendreihundertvierundsechzigtausendsiebenhundertacht)
Was haben all diese Zahlen gemeinsam?
- Natürliche Zahlen kannst du ohne Komma und Bruchstrich darstellen.
- Es gibt unendlich viele Natürliche Zahlen.
- Wenn du zwei Natürliche Zahlen miteinander addierst oder multiplizierst, erhältst du als Ergebnis wieder eine Natürliche Zahl.
Beispiel: 17+12=29 oder 3⋅17=51.
Beim Subtrahieren erhältst du nur dann wieder eine natürliche Zahl, wenn du eine kleinere von einer größeren Zahl abziehst, z. B.
42-35=7.
Du kannst den Wert einer natürliche Zahl über einen Zahlenstrahl veranschaulichen. Dabei gilt, je weiter rechts eine Zahl auf dem Zahlenstrahl liegt, desto größer ist ihr Wert.

Von den Natürlichen Zahlen zu den Bruchzahlen
Was passiert, wenn du zwei Natürliche Zahlen dividierst?
Teilst du 8 Äpfel auf 2 Personen auf, erhält jeder82=4 Äpfel.
Möchtest du nun 9 Äpfel auf 2 Personen aufteilen, bekommt jeder wieder 4 Äpfel, aber 1 Apfel bleibt übrig.

Um gleichmäßig aufzuteilen, musst du diesen halbieren, so dass jeder 12 Apfel dazu bekommt.
So kommst du schnell in die Welt der Bruchzahlen und erkennst:
92=412
Diese Zahl liegt zwischen zwei benachbarten Natürlichen Zahlen, nämlich zwischen der 4 und der 5.
Nun kann man den Zwischenraum zweier benachbarter Natürlicher Zahlen in beliebig viele Stücke aufteilen - dort liegen also unendlich viele Bruchzahlen!

Die Anzahl der gleichgroß aufgeteilten Stücke liefert den Nenner einer Bruchzahl. Der Zähler gibt an, am wievielten Abschnitt die jeweilige Zahl liegt.
Besonderheiten der Bruchzahlen
Du weißt bereits, wie sich Bruchzahlen am Zahlenstrahl darstellen lassen. Auch für die Bruchzahlen gilt: je weiter rechts eine Zahl auf dem Zahlenstrahl liegt, desto größer ist ihr Wert.
Aber Achtung: unterschiedliche Bruchzahlen können denselben Wert haben!
Beispiel: 12 und 24

Die beiden Bruchzahlen liegen an exakt selben Stelle - klar, denn du könntest 24 ja auch durch 2 kürzen, und Kürzen verändert den Wert einer Zahl nicht!
Daher gibt es auch Bruchzahlen, die den Wert einer natürlichen Zahl annehmen, z.B.
93=3, oder 44=1, oder 5427=2, …

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Der Wert einer Bruchzahl
Um dir den Wert einer Bruchzahl zu verdeutlichen, vergleichst du am besten Zähler und Nenner:
Ist der Zähler kleiner als der Nenner, so ist der Wert des Bruchs kleiner als 1.
Ist der Zähler größer als der Nenner, ist auch der Wert des Bruchs größer als 1.
Sind Zähler und Nenner gleich, hat die Bruchzahl den Wert 1.
Um den genauen Wert einer Bruchzahl zu bestimmen, kannst Du einfach schriftlich dividieren:
34=3:4=0,75 oder 105=2
Ist der Zähler ein Vielfaches des Nenners, so hat der Bruch den Wert einer Natürlichen Zahl!
Du kannst Brüche auch geschickt aufteilen, um einfacher zu rechnen:
94=8+14=84+14=2+14=2,25
Das „Aufteilen“ hilft dir auch, die Größe einer Bruchzahl richtig abzuschätzen:
257=21+47=217+47=347
Damit weißt du, dass der Wert von 257 zwischen 3 und 4 liegt.

Vergleich von zwei Bruchzahlen
Du kannst auch leicht ohne Rechnung entschieden, welcher von zwei Brüchen den größeren oder kleineren Wert hat.
1.Fall: Beide Brüche haben denselben Nenner
Beispiel: 38 und 58
Stell dir eine Pizza vor: Du teilst sie jeweils in Achtel, einer isst 3 Anteile, und der andere 5 Anteile - wer hat weniger gegessen?

So wird schnell klar, dass der Wert von 38 kleiner ist als 58 , und du kannst schreiben: 38<58.
Haben zwei Brüche denselben Nenner, hat der Bruch mit dem größeren Zähler den höheren Wert!
Der Vergleich von Brüchen
2.Fall: Beide Brüche haben denselben Zähler
Beispiel: 512 und 510
Stell dir wieder eine Pizza vor: Du teilst einmal in 12 Stücke auf, das andere mal in 10, nimmst aber jeweils 5 Anteile.

Die Zwölftel sind natürlich kleiner als die Zehntel, und so wird schnell klar, dass 512 kleiner als 510 ist.
Auf dem Zahlenstrahl liegt 512 also weiter links als 510.

Haben zwei Brüche denselben Zähler, so hat der Bruch mit dem größeren Nenner den kleineren Wert.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Der Vergleich von Brüchen
3.Fall: Weder Zähler noch Nenner sind gleich
In diesem Fall solltest du die Brüche zunächst soweit wie möglich kürzen.
Beispiel: 57 und 49
Möglichkeit A: Zahlenstrahl
Du kannst die Brüche wie gehabt auf dem Zahlehnstrahl eintragen und vergleichen. Aber je größer der Nenner wird oder je dichter die Werte der Brüche beisammen liegen, desto schwieriger wird dieser Weg.

Möglichkeit B: Hauptnenner finden
Durch geschicktes Kürzen oder Erweitern bringst du beide Brüche auf einen Hauptnenner und vergleichst die Zähler. Wie du schon weißt gilt: bei gleichem Nenner ist der Bruch mit dem größeren Zähler auch größer.
Beispiel: 57=4563 und 49=2863, der erste Bruch ist also größer!
Möglichkeit C: Überschlagsrechnung
Mit dem Zähler- und Nennervergleich kannst du häufig die Größe der Bruchzahlen auch einfach schätzen:
Im Beispiel ist 57 größer als 3,57=12, und 49 ist ein bisschen kleiner 4,59=12. Der erste Bruch ist also größer als als der zweite!
Gemeinsamkeiten und Unterschiede
Du hast gesehen, dass es unendlich viele natürliche Zahlen und auch unendlich viele Bruchzahlen gibt. In beiden Zahlenräumen kannst du addieren, multiplizieren, und kleinere Zahlen von größeren Zahlen subtrahieren. Doch es gibt auch Unterschiede!
1. Jede Natürliche Zahl lässt sich als Bruchzahl schreiben
Darf gibt es viele Möglichkeiten, da du kürzen kannst, wie im Beispiel 2=42=105=5427. Umgekehrt geht dies jedoch nicht!
2. Bei der Division von Bruchzahlen erhältst du immer eine Bruchzahl
Dieses Ergebnis kannst du vielleicht sogar kürzen und eine natürliche Zahl erhalten, wie bei 62=3. Wenn du allerdings natürliche Zahlen dividierst, „fällst“ du manchmal aus den Natürlichen Zahlen heraus und landest in den Bruchzahlen, wie z.B. bei 6:5=65=1,2!
3. Zwischen zwei Bruchzahlen liegt immer eine weitere Bruchzahl
Egal, wie nahe zwei Bruchzahlen nebeneinander liegen: Du findest dazwischen immer noch eine Bruchzahl!
Beispiel: Nimmst Du 57 und 67, dann kannst du einfach den Nenner vergrößern und die Bruchzahl „zwischen“ den beiden Brüchen nehmen: 57=1014 und 67=1214, und du siehst sofort: 1114 liegt zwischen den Brüchen!
Bei Natürlichen Zahlen geht das nicht, denn jede Natürliche Zahl hat genau einen Nachfolger: 1,2,3,…42,43,….
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen