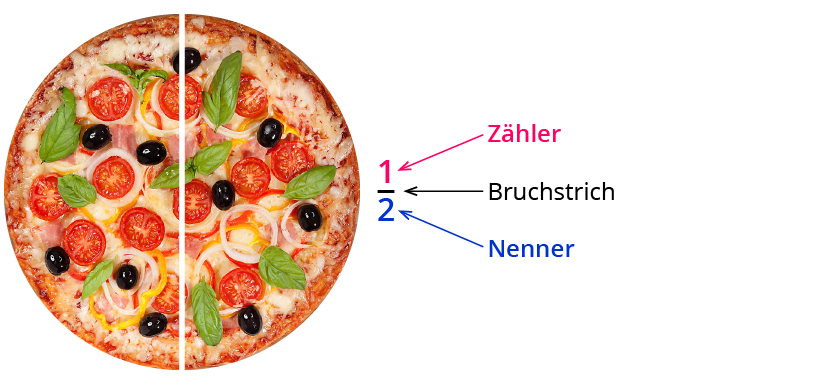
Bruchteile erweitern und kürzen
Erweitern und Kürzen
Du weißt schon, dass Brüche verschiedene Namen, aber trotzdem den gleichen Wert haben können.

Zwischen den verschiedenen Bruchzahlen gibt es bestimmt einen Zusammenhang? Klar, los geht’s:
Kürzen
Guckst du dir die Bilder der beiden Brüche an, fällt dir auf, dass im Bild rechts Einteilungsstriche fehlen. Es handelt sich um eine Vergröberung der Einteilung.

Siehst du dir die Brüche 28 und 14 genauer an, fällt dir auf, dass Zähler und Nenner des ersten Bruchs durch 2 dividiert worden sind.
28=2:28:2=14
Dieses Vorgehen heißt Kürzen.
Eine Schreibweise für das Kürzen sieht so aus:
2
Sie bedeutet: 28 wird gekürzt mit 2. Die Zwei steht unter dem Gleichheitszeichen. Sie bedeutet, dass du Zähler und Nenner des ersten Bruchs durch Zwei dividierst.
Durch das Kürzen eines Bruchs ändert sich der Wert des Bruchs nicht.
Die Kürzungszahl
Kürzen kannst du mit jeder Zahl, wenn du durch Division wieder eine ganze Zahl in Zähler und Nenner herausbekommst.

Du kannst bei dieser Aufgabe nicht mit 5 kürzen, denn dann bekommst du unüblich:
5
Mathematisch ist das richtig, aber du redest nicht vom Kürzen, wenn du eine Dezimalzahl erhältst.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Erweitern
Das Erweitern ist die Umkehrung zum Kürzen. Du verfeinerst einen Bruch.

Du multiplizierst Zähler und Nenner mit derselben Zahl.
Ausführlich aufgeschrieben sieht das so aus:
14=1⋅24⋅2=28
Eine Schreibweise für das Erweitern sieht so aus:
142=28
Die Zwei auf dem Gleichheitszeichen bedeutet, dass du Zähler und Nenner mit der Zwei multiplizierst.
Beim Erweitern ändert sich der Wert des Bruches nicht.
Erweiterungszahlen
Du kannst einen Bruch mit jeder natürlichen Zahl größer als 1 erweitern.

23 3= 69
Kürzen mit Rechtecken
Du kannst das Kürzen und Erweitern auch an Rechtecken darstellen.
Beispiel: Kürzen mit 2

Mathematisch :
620=6:220:2=310
Oder kurz:
2

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Erweitern bei Strecken
Du kannst das Kürzen und Erweitern auch an Strecken darstellen.
Beispiel: Erweitern mit 3

133→39
Mathematisch:
13=1⋅33⋅3=39
Oder kurz:
133=39
Kürzen bis zur Grunddarstellung
Du kannst einen Bruch mehrmals kürzen, wenn die Zahlen das zulassen.

Lässt sich ein Bruch nicht weiter kürzen, heißt dieser Bruch „Grunddarstellung“ des Bruches.
Wenn du die größtmögliche Zahl, mit der du kürzen könntest, gleich siehst, kannst du in einem Schritt kürzen.
Beispiel:

Dir helfen die Teilbarkeitsregeln beim Finden der höchsten Kürzungszahl.
Teilbarkeitsregeln
Eine Zahl ist durch 2 teilbar, wenn ihre letzte Stelle durch 2 teilbar ist. (Endstelle 0, 2, 4, 6, 8)
Eine Zahl ist durch 5 teilbar, wenn ihre letzte Stelle eine 0 oder 5 ist.
Eine Zahl ist durch 10 teilbar, wenn ihre letzte Stelle eine 0 ist.
Eine Zahl ist durch 3 teilbar, wenn ihre Quersumme (alle Ziffern +) durch 3 teilbar ist.
Eine Zahl ist durch 9 teilbar, wenn ihre Quersumme (alle Ziffern +) durch 9 teilbar ist.
Sonderfälle 1 und 0
Das Erweitern mit der Zahl 1 führt zu keinem neuen Bruch. Deswegen führst du das nicht durch. Das Kürzen mit 1 führt ebenfalls zu demselben Bruch. Auch das ist überflüssig, aber möglich.
1
Das Erweitern mit 0 ist unsinnig. Wenn du eine Zahl mit 0 multiplizierst, kommt 0 als Ergebnis heraus. Kürzen mit 0 ist mathematisch nicht richtig. Durch 0 dividieren führt zu keinem Ergebnis.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Primfaktorzerlegung und Kürzen
Wenn du ganz professionell vorgehen willst, wendest du die Primfaktorzerlegung von Zähler und Nenner an.
Du schreibst Zähler und Nenner in Primfaktoren aus. Alle Primfaktoren, die sowohl im Zähler als auch im Nenner zu finden sind, sind Kürzungszahlen. Multiplizierst du alle miteinander, erhältst du die größtmögliche Kürzungszahl.

Gemeinsame Primfaktoren
Primfaktor
Du kannst jede Zahl in ihre Primfaktoren zerlegen und als Multiplikationsaufgabe ausdrücken. Beispiel:
12=2⋅2⋅3
2 und 3 sind Primzahlen.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen