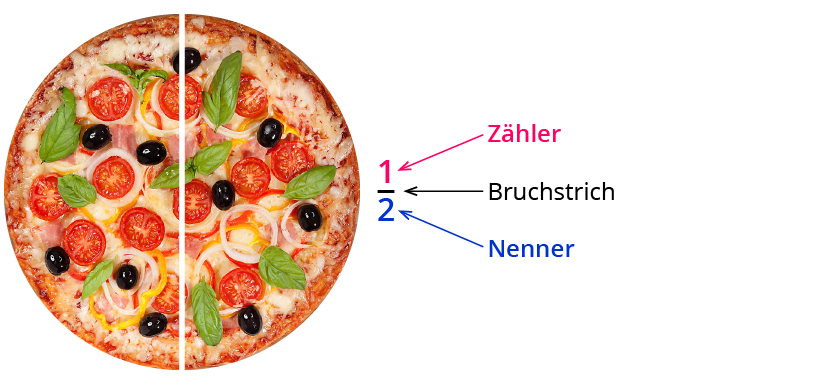
Bruchteile vergröbern und verfeinern
Ein Bruch - viele Namen
Sieh dir diese Bilder von Brüchen an.

In jedem Kreis ist dieselbe Fläche ausgemalt. Die Brüche tragen aber verschiedene Namen.

Verfeinern und Vergröbern
Mathematisch heißt das: Du kannst einen Bruch verfeinern oder vergröbern.

Brüche können unterschiedliche Namen, aber denselben Wert haben.
Bildlich gesprochen: Die Fläche, die der Bruchteil einnimmt, ist dieselbe, obwohl der Bruch andere Zahlen besitzt.
Verfeinern geht immer
Das Verfeinern eines Bruchs kannst du immer anwenden.
Das kannst du dir so vorstellen, dass du das Ganze in kleinere gleich große Teile zerlegst. Im Bild zeichnest du die Verfeinerung einfach ein.
Beispiel 1
Du hast 14. Zeichne die roten Striche ein und du hast 28.

Jedes Viertel des Ganzen wurde in zwei gleich große Teile geteilt.
Beispiel 2
Du hast wieder 14. Zeichne die roten Striche ein und du hast 312.

Jedes Viertel des Ganzen wurde in drei gleich große Teile geteilt.
Du kannst das Viertel in beliebig viele gleich große Teile zerlegen.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Ein bisschen rechnen
Wie verändern sich beim Verfeinern Zähler und Nenner?
Zerlegst du zum Beispiel das Viertel in zwei Teile, verfeinerst du mit 2.

Du rechnest:

Der Fachbegriff für diese Rechnung heißt Erweitern.
Vergröbern
Das Vergröbern ist die Umkehrung zum Verfeinern. Bildlich gesprochen radierst du Striche weg.
Du gehst von einem Bruch aus, bei dem eine feine Einteilung vorliegt. Dann entfernst du Striche so, dass weiter gleich große Stücke entstehen.
Beispiel
Du hast 39. Entferne die Mittelstriche. Es bleibt eine Dritteleinteilung. Du hast den Bruch 13.

Wieder gerechnet
Wie verändern sich beim Vergröbern Zähler und Nenner?
Machst du aus 3 Teilen 1 Teil, vergröberst du mit 3.

Der Fachbegriff für diese Rechnung heißt Kürzen.
Wieso durch 3 rechnen? Du radierst doch nur 2 Striche weg? Entscheidend ist aber, dass du aus 3 Teilen 1 größeres Teil machst. Deshalb rechnest du durch 3.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Vergröbern geht nicht immer
Du kannst den Bruch 39 nicht so vergröbern, dass du jeden zweiten Strich entfernst. Denn so entstehen keine gleich großen Teile.

Vergröbern geht nur, wenn du Zähler und Nenner durch die Vergröberungszahl ohne Rest teilen kannst.
Andere Darstellungen
Du kannst Vergröbern und Verfeinern auch in anderen Darstellungen verdeutlichen.
Beispiel Verfeinerung einer Strecke:

Beispiel Vergröberung eines Rechtecks:

Du könntest 2472 auch mit 12 vergröbern. Der Bruch heißt dann 26.

Oder du vergöberst mit 24. Der Bruch heißt dann 13.

Beispiel Vergröberung eines Körpers:
Auch an Körpern kannst du Vergröbern und Verfeinern darstellen. In diesem Beispiel wird vergröbert.

kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen