Brüche dividieren (Kehrwertregel)
Die Division von Brüchen
Du weißt, was Brüche sind und kannst sie addieren, subtrahieren, multiplizieren und einen Bruch durch eine natürliche Zahl dividieren. Fehlt noch? Die Division von zwei Brüchen!
Zur Erinnerung hier noch mal die wichtigsten Regeln! Dann wird dir die Regel für’s Dividieren leichter fallen!
| REGEL | Beispiel |
|---|---|
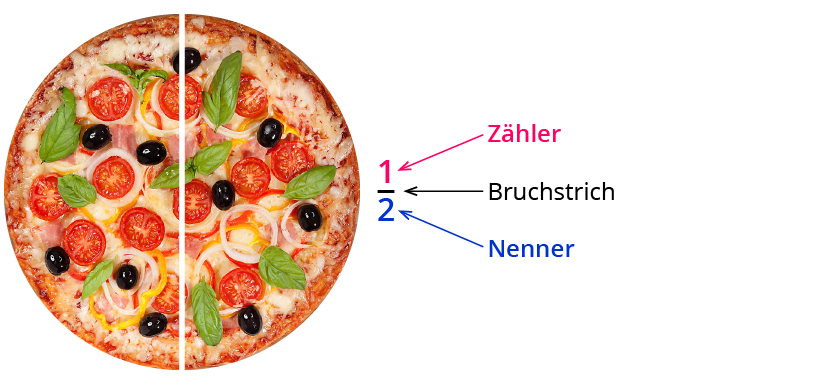
| Ein Bruch besteht aus einem Zähler und einem Nenner: ZÄHLERNENNER | |
| Du multiplizierst zwei Brüche, indem du jeweils die Zähler und Nenner multiplizierst. Oder kurz: ZÄHLER mal ZÄHLER und NENNER mal NENNER | 12⋅34=1⋅32⋅4 =38 |
| Du dividierst einen Bruch durch eine natürliche Zahl, indem du den Nenner des Bruchs mit der Zahl multiplizierst und den Zähler beibehältst | 45:3=4(5⋅3) =415 |
Was bedeutet es, zwei Brüche zu dividieren?
Die Aufgabe: 34:38
Das bedeutet:
Wie oft passt der Bruchteil 38 in den Bruchteil 34?
Als Bild:

Verschiebe das 38-Tortenstück und überlege, wie es in die Fläche von 34 hineinpasst.
Es passen genau 2 von der 38-Torte in die 34-Torte:

Die Rechnung heißt also: 34:38=2
Erinnerst du dich? Auch bei der Division von ganzen Zahlen, hast du dich gefragt, wie oft eine Zahl in eine andere hineinpasst.
8:2=4 hat dir gesagt, dass die 2 genau 4 mal in die 8 passt
Ein Beispiel, wenn es nicht so gut passt
Die Aufgabe: 69:36
Das bedeutet: Wie oft passt der Bruchteil 36 in den Bruchteil 69?
Stelle es dir bildlich vor:

Verschiebe den 36-Block: Der Block passt ein ganzes mal hinein und zusätzlich noch zu einem Bruchteil von 13. Die 36 passen 113 mal in 69.

Die Aufgabe heißt: 69:36=113=43

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Findest du schon die Regel?
Versuche, von den Beispielen eine Regel abzuleiten:

Der ZÄHLER des Ergebnisses ergibt sich aus der Multiplikation des Zählers des einen mit dem Nenner des anderen Bruchs.
Der NENNER ergibt sich aus der Multiplikation des Nenners des einen mit dem Zähler des anderen Bruchs.
In kurz das 3. Beispiel: 69:36=69⋅63=6⋅69⋅3=3627
Du verwandelst die Divisionsaufgabe in eine Malaufgabe! Dazu drehst du den zweiten Bruch um. Mathematisch heißt das: Du bildest den Kehrwert des Bruchs.
Du dividierst zwei Brüche, indem du den ersten Bruch mit dem Kehrwert des zweiten Bruches multiplizierst.
Beispiel: 53:72=53⋅27=5⋅23⋅7=1021
Der Kehrwert:
Zu jedem Bruch gibt es einen wertvollen Partner: den Kehrbruch oder Kehrwert. Vertausche Zähler und Nenner und du erhältst den Kehrwert.
Der Kehrwert von 23 ist 32.
Der Kehrwert von 5=51 ist 15.
Beispiele, Beispiele
23:12=23⋅21=2⋅23⋅1=43
56:27=56⋅72=3512
Und mit Kürzen
Geschicktes Kürzen ist immer gut.:-)
117:2235=117⋅3522=1⋅51⋅2=52
2415:1625=2415⋅2516=6⋅53⋅4=2⋅51⋅4=1⋅51⋅2=52
Kürze erst, wenn du die Divisionsaufgabe in die Mal-Aufgabe umgewandelt hast.
Division von gemischten Zahlen
Gemischte Zahlen wandelst du wie beim Multiplizieren erst mal in einen unechten Bruch um.
Beispiel:
213:523=73:173=73⋅317=717
Beispiel 2: mit Kürzen
445:3610=245:3610=245⋅1036=2⋅21⋅3=43=113

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Doppelbrüche
Erinnerst du dich: Ein Bruch ist nichts anderes als eine Divisionsaufgabe.
12=1:2=0,5 oder 34=3:4=0,75
Das brauchst du bei Doppelbrüchen. Doppelbrüche? Die haben im Zähler und im Nenner einen Bruch.
Beispiele:
3458=34:58=34⋅85=65
10492=104⋅29=1018=59
Wozu brauchst du die Division von Brüchen?
Die Division brauchst du, wenn du einen Bruchteil gleichmäßig aufteilst.
Beispiel:
In einer Flasche sind 34 Liter Saft. Wie viel Gläser zu je
150ml (320 Liter) kannst du damit füllen?
Lösung:
34:320=34⋅203=5
Antwort: Du kannst genau 5 Gläser füllen.

kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen