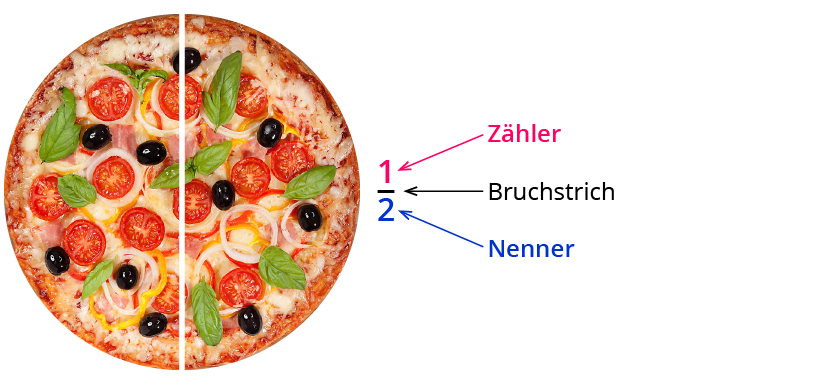
Brüche ordnen
Mehr oder weniger?
Ganz wichtig: Auf welchem Blech gibt’s mehr Pizza zu essen?:-)

Welcher Bruchteil ist größer? Mit Augenmaß zu schätzen, ist schon schwierig. Und den Brüchen siehst du auch nicht gleich an, welcher größer ist.
Jetzt lernst du verschiedene Methoden kennen, wie du berechnen kannst, welcher Bruch größer ist. Damit kannst du Brüche vergleichen und ordnen.
Erst mal vergleichst du zwei Brüche. Die Verfahren funktionieren aber bei mehreren Brüchen genauso.
Brüche mit demselben Nenner
Brüche mit demselben Nenner kannst du ganz einfach vergleichen. Du guckst, welcher Zähler größer ist. Dieser Bruch ist der größere.
Beispiel: Vergleiche 67 und 47.
67>47
Das heißt: 67 ist größer als 47.
Bildlich sieht es so aus:

67 > 47
Zum Vergleichen von Zahlen gibt es die Zeichen
< kleiner als
> größer als
= gleich
„kleiner“ und < kannst du dir gut merken:

Ein Bruch bedeutet: Teile das Ganze in so viele Teile wie der Nenner vorgibt. Nimm so viele Teile davon, wie der Zähler vorgibt.
Beispiel:
Teile das Ganze in VIER Teile. Nimm DREI davon.

Brüche mit demselben Zähler
Brüche mit demselben Zähler kannst du auch auf einen Blick vergleichen.
Beispiel: Vergleiche 45 und 46.
45>46
Das erkennst du im Bild.

45 > 46
45 sind mehr, weil das Ganze in weniger Teile geteilt wird. Sind die Zähler gleich, ist der Bruch mit dem größeren Nenner der kleinere.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Beliebige Brüche
Was ist nun aber mit Brüchen, bei denen Zähler und Nenner verschieden sind?
Beispiel: Vergleiche 920 und 2350.
Gehe so vor:
1. Den gleichen Nenner suchen:
Du bringst die Brüche, die du ordnen willst, auf denselben Nenner.
Suche eine Zahl, die sowohl in der Vielfachreihe von 20 als auch in der Vielfachreihe von 50 vorkommt.
20,40,60,80,100,120,…
50,100,150,…
Du siehst, dass die 100 in beiden Vielfachreihen vorkommt.
2. Erweiterungszahlen bestimmen:
100:20=5. Die 100 steht an der 5. Stelle der Vielfachreihe.
100:50=2. Die 100 steht an der 2. Stelle der Vielfachreihe.
3. Erweitern:
Erweitere 920 so, dass im Nenner die 100 steht.
100100
Jetzt erweiterst du 2350 so, dass im Nenner die 100 steht.
100100
4. Vergleichen:
Jetzt vergleichst du die beiden Zähler. Der Bruch mit dem größeren Zähler ist der größere Bruch.
46100>45100
Also 2350>920.
Du vergleichst Brüche mit unterschiedlichen Zählern und Nennern, indem du sie auf denselben Nenner bringst.
So gehst du vor:
- Den gleichen Nenner suchen
- Erweiterungszahlen bestimmen
- Erweitern
- Vergleichen
Wenn du dich jetzt fragst, ob du die Brüche nicht auch auf denselben Zähler bringen könntest, ist die Antwort JA.
Allerdings bringen die wenigsten Menschen Brüche auf denselben Zähler. Ist aber mathematisch richtig.
Pizza!!
Auf welchem Blech ist denn nun mehr Pizza?

1. Den gleichen Nenner suchen:
15 30 45 60 75
12 24 36 48 60 – ah, die 60!
2. Erweiterungszahlen bestimmen:
60:15=4
60:12=5
3. Erweitern:
8154=3260
7125=3560
4. Vergleichen:
3260<3560
Also: 815<712
Schnapp dir das zweite Pizza-Blech.:-)
Wenn du schon Dezimalbrüche kennst
Du rechnest die zu ordnenden Brüche in eine Dezimalzahl um. Dann kannst du sie einfach vergleichen.
Beispiel: Vergleiche 920 und 2350.
920=9:20=0,45
-0
¯90
-80
¯100
-100̲
0
2350=23:50=0,46
- 0
¯230
-200
¯300
-300̲
0
Wenn du 0,45 und 0,46 vergleichst, siehst du, dass 0,46 die größere Zahl ist. (6 ist mehr als 5.)
Wenn du die beiden Brüche in den Taschenrechner eingibst, erhältst du auch diese Dezimalzahlen.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Unechte Brüche
Bei Brüchen größer als 1 funktioniert das Ordnen genauso wie bei echten Brüchen. Allerdings gibt es den Fall, dass du gar nicht rechnen musst, wenn du auf den ersten Blick siehst, welcher Bruch größer ist.
Beispiel: Welcher Bruch ist größer? 23 oder 65?
23 ist kleiner als ein Ganzes. Das erkennst du daran, dass der Zähler eine kleinere Zahl besitzt als der Nenner. 65 ist größer als ein Ganzes. Du könntest auch 115 dafür schreiben.
Also weißt du gleich: 65>23
Trick: Stützgröße 12
Wenn du zwei Brüche gegeben hast, bei denen einer größer als 12 und einer kleiner als 12 ist, kannst du dir das Rechnen sparen.
Beispiel: Welcher Bruch ist größer? 23 oder 37
23 ist mehr als 12.
37 ist weniger als 12.
Jetzt kannst du angeben:
23>37
Oder
37<23
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen