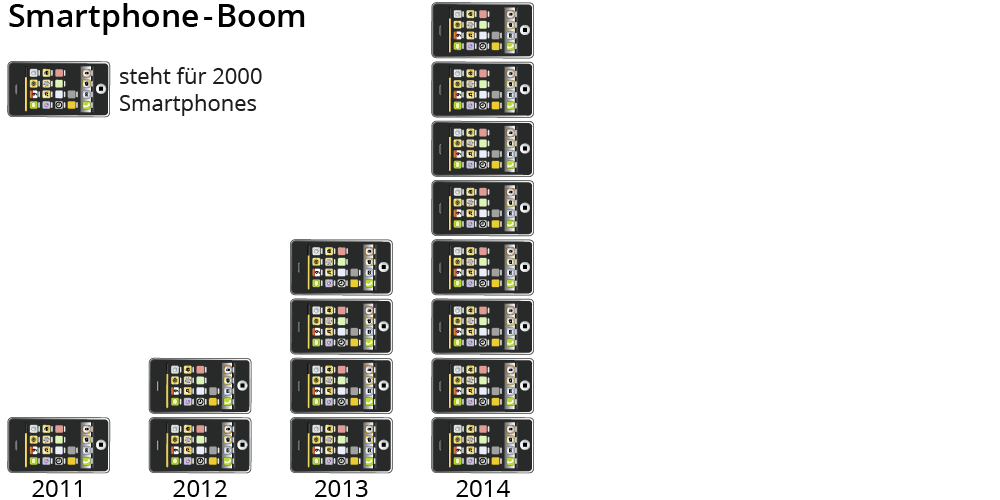
Relative Häufigkeiten
Toooor!!
Fußball ist nicht nur was für Jungs. :-) Hier sind 2 Mädels, die Fußball spielen:

Was meinst du: Welches der Mädchen ist treffsicherer?
Das kannst du gar so schnell ablesen? Richtig!
Ida hat mehr Tore geschossen, nämlich 8. Aber es macht einen Unterschied, ob sie in 8 von 20 Einsätzen trifft oder in 8 von 100 Einsätzen.
Dich interessiert also nicht die absolute Zahl 8, sondern wieviel diese 8 Treffer von den gesamten Einsätzen ausmachen.
Mathematiker nennen das absolute und relative Häufigkeit.
Die absolute Häufigkeit gibt hier die Anzahl der geschossenen Tore an. Da liegt Ida vorne. Sie hat 8 Tore erzielt, Carla nur 6.
Die relative Häufigkeit gibt den Anteil der erzielten Tore bezogen auf die Gesamtzahl der Einsätze an.
Die relative Häufigkeit berechnest du: ToreGesamtzahl der Einsätze.
| Carla | Ida | |
|---|---|---|
| absolute Häufigkeit (Tore) | ||
| Gesamtzahl (Einsätze) | ||
| relative Häufigkeit / Anteil | 612=12=0,5 | 820=410=0,4 |
Absolut hat Ida mehr Tore geschossen als Carla.
Relativ hat Carla den größeren Anteil an Toren bezogen auf die Anzahl ihrer Einsätze geschossen.
Carla ist also treffsicherer als Ida.
Absolute und relative Häufigkeiten
Wenn du Daten vergleichen willst, brauchst du nicht nur die absolute, sondern auch die relative Häufigkeit.
Als Formel sieht das so aus:
relative Häufigkeit=absolute HäufigkeitGesamtzahl
Beispiel mit Kugeln:
Du hast ein Gefäß mit diesen Kugeln:

Bestimme die absolute und relative Häufigkeit der roten und der blauen Kugeln.
Gesamtzahl Kugeln: 10
Rote Kugeln:
absolute Häufigkeit: 6
relative Häufigkeit: 610=0,6
Blaue Kugeln:
absolute Häufigkeit: 4
relative Häufigkeit: 410=0,4
Die absolute Häufigkeit ist eine Anzahl. Damit wird gezählt, wie oft etwas vorkommt.
Die relative Häufigkeit ist der Anteil an einer Gesamtzahl. Du schreibst sie als Bruch oder Dezimalbruch.
Die relative Häufigkeit eines Ergebnisses ist der Quotient aus der absoluten Häufigkeit und der Gesamtzahl: relative Häufigkeit=absolute HäufigkeitGesamtzahl
Relative Häufigkeiten kannst du sowohl in Brüchen, Dezimalbrüchen als auch in Prozent (%) angeben.
Beispiel: 14=25100=0,25=25%
Kleine Wiederholung: Brüche in Dezimalbrüche umwandeln
Relative Häufigkeiten schreibst du erstmal als Bruch auf.
Aber manchmal sind Dezimalbrüche praktischer.
Du erweiterst oder kürzt den Bruch, bis du unten im Nenner eine 10, eine 100 oder eine 1000 hast. So einen Bruch kannst du dann als Dezimalbruch schreiben.
Beispiele:
352=3⋅25⋅2=610=0,6
1254=1⋅425⋅4=4100=0,04
3
Manche Brüche hast du auch schon im Kopf:
- 12=0,5
- 14=0,25
- 34=0,75

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Relative Häufigkeiten und Diagramme
Relative Häufigkeiten kannst du auch in Diagrammen darstellen.
Beispiel:
Hast du auch schon mal Glücksrad gespielt? Und was gewonnen? :-)
So kann ein Glücksrad aussehen:

Wenn 200 Leute am dem Glücksrad drehen, kann dieses Ergebnis herauskommen:
| absolute Häufigkeit | relative Häufigkeit | |
|---|---|---|
| rot | 50 | 50200=14=0,25 |
| orange | 50 | 50200=14=0,25 |
| blau | 100 | 100200=12=0,5 |
So sieht das Säulendiagramm dazu aus:

Summenprobe
Anna würfelt mit einem Würfel 100 mal. Sie trägt die
Ergebnisse in eine Häufigkeitsliste ein:
| Ergebnis | absolute Häufigkeit | relative Häufigkeit |
|---|---|---|
| 19100=0,19 | ||
| 16100=0,16 | ||
| 18100=0,18 | ||
| 17100=0,17 | ||
| 15100=0,15 | ||
| 19100=0,15 |
Rechne mal die Summen der absoluten und relativen Häufigkeiten aus:
Absolute Häufigkeiten: 19+16+18+17+15+15=100
Du erhältst die Gesamtzahl, hier Annas 100 Würfe.
Relative Häufigkeiten:
0,19+0,16+0,18+0,17+0,15+0,15=1
Du erhältst 1.
Das ist immer so! Diese Regel heißt Summenprobe und du kannst sie als Kontrolle benutzen.
Addierst du alle absoluten Häufigkeiten, kommt immer die Gesamtzahl heraus.
Addierst du alle relativen Häufigkeiten, kommt immer 1 heraus.

Die Summenprobe als Rechenkontrolle kann dann von 1 abweichen, wenn die relativen Häufigkeiten gerundete Werte sind.
Wenn du die Summe der relativen Häufigkeiten bildest, erhältst du folgendes Ergebnis:
0,19+0,16+0,18+0,17+0,15+0,15=1
Dieses Ergebnis gilt allgemein. Du kannst daher diese Regel, genannt Summenprobe auch als Kontrolle benutzen.
Die Summenprobe als Rechenkontrolle kann dann von 1 abweichen, wenn die relativen Häufigkeiten gerundete Werte sind.
Runden…
Beispiel: 6 Apps für Kinder
Bei einer Umfrage wurden 150 Personen nach beliebten Apps für Kinder befragt. Hier ist das Ergebnis. Die Dezimalbrüche sind gerundet.
| App | absolute Häufigkeit | relative Häufigkeit |
|---|---|---|
| Muh-Box | ||
| Little Winzki | ||
| Mini Piano | ||
| Kids Paint | ||
| memory Kids | ||
| English is Easy |
Führe die Summenprobe für die relativen Häufigkeiten durch:
0,17+0,23+0,12+0,15+0,19+0,13=0,99
Oh, da kommt gar nicht 1 raus!!
Wenn du aber die relativen Häufigkeiten in der Bruchschreibweise addierst, erhältst du wieder als Summe 1:
26150+35150+18150+23150+28150+20150=150150=1
Das Problem ist, dass du bei den Dezimalbrüchen manchmal runden musst. Wenn du mit den gerundeten Zahlen weiter rechnest, bekommst du ungenaue Ergebnisse. Am sichersten rechnest du mit Brüchen.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen