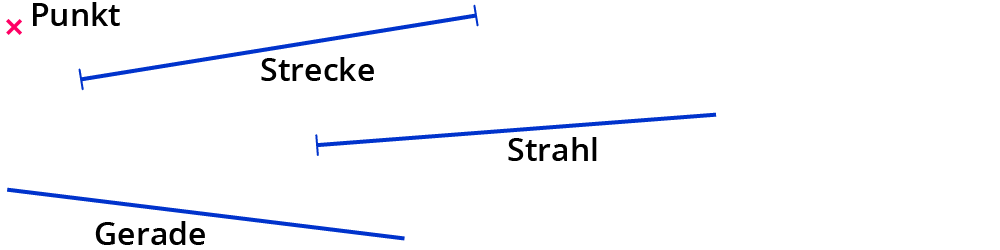
Strecke Gerade und Strahl / Halbgerade
Das Einmaleins der Geometrie
Beim Rechnen gibt’s das kleine Einmaleins. In der Geometrie gibt es diese 4 Objekte, die du immer brauchst:
- Punkt
- Strecke
- Strahl / Halbgerade
- Gerade

Guck dir genauer ihre Eigenschaften an:
Der Punkt
Einen Punkt kennst du aus der Rechtschreibung. Jeder Satz endet mit einem Punkt.
Der mathematische Punkt
In der Mathematik ist ein Punkt die kleinste geometrische Bedeutungseinheit. Eigentlich ist ein Punkt so klein, dass du ihn nicht sehen kannst. Damit das nicht passiert, haben Mathematiker entschieden, den Punkt mit einem x zu kennzeichnen. Der Punkt ist genau da, wo sich die 2 Striche des x kreuzen.
Punkte werden in Zeichnungen mit großen Buchstaben gekennzeichnet.
Beispiel:

Die Beschriftung für einen Punkt notierst du schräg versetzt neben dem x.
In Figuren gibt es auch Eckpunkte. Die Eckpunkte brauchst du nicht mit einem x zu markieren. Der Punkt ist da, wo die Begrenzungslinien (Seiten) der Figur zusammenstoßen.

Einen Punkt markierst du mit einem x.
Die Strecke
Die Strecke kennst du aus deinem Leben, wenn es darum geht: „Welches ist die kürzeste Strecke zur Schule?“ oder „Wie lang ist die Strecke noch?“
Beide Fragen meinen aber nicht die mathematische Strecke. Mit der kürzesten Strecke zur Schule ist eigentlich der kürzeste Weg gemeint. Es geht darum, möglichst schnell zur Schule zu kommen. Du benutzt Kurven und Kreuzungen auf deinem Weg.
Wenn dich die Länge einer Strecke interessiert, willst du wissen, wie lange du unterwegs bist. Du fragst also eigentlich nach der Zeit.
Die mathematische Strecke
Die mathematische Strecke bezeichnet die kürzeste Verbindung zwischen zwei Punkten.
Wichtig: Eine Strecke ist die „kürzeste Verbindung“. Eine Strecke besitzt keine Kurve.
Beispiel:
Erst hast du die beiden Punkte.

Verbinde die Punkte und du erhältst die Strecke.

Üblicher ist diese Darstellung:

Die Strecke hat meistens einen Kleinbuchstaben als Namen.

Ganz genau kannst du für die Strecke von A nach B auch ¯AB schreiben. Der Strich über den Buchstaben zeigt dir, dass es sich um eine Strecke handelt. Es ist egal, wie herum du die Buchstaben notierst, aber in der Regel beginnst du mit dem Buchstaben, der vorn im Alphabet steht.
Eine Strecke ist die kürzeste Verbindung zwischen 2 Punkten. Die Länge einer Strecke kannst du messen.
Die Länge der Strecke ¯AB schreibst du so: |AB|=3 cm.

Der Begriff „Luftlinie“ bezeichnet die kürzeste Verbindung zwischen zwei Orten. Das ist damit eine Strecke.
Eine Strecke, die eine Figur begrenzt, hat den Namen Seite. Eine Strecke, die einen Körper begrenzt, heißt Kante.
Der Strahl / Die Halbgerade
Den Begriff „Strahl“ kennst du zum Beispiel vom Sonnenstrahl oder Lichtstrahl.
Wenn du dir einen Sonnenstrahl vorstellen kannst, geht er von der Sonne weg. Er geht immer weiter, bis er auf die Erde trifft.

Bild: Panther Media GmbH (dzmitri mikhaltsow)
Der mathematische Strahl
Ein mathematischer Strahl geht auch von einem Punkt aus. Allerdings hat er kein Ende. Das bedeutet, dass er bis ins Unendliche weitergeht.
Du kennst schon den Zahlenstrahl. Er geht oft bei 0 los und geht theoretisch bis ins Unendliche weiter.
Du kannst keinen unendlichen Strahl zeichnen. Deswegen haben sich Mathematiker eine Darstellungsart überlegt, die als Symbol für die unendliche Linie steht.
Beispiel für einen Strahl:
Am Anfang steht auch hier der Punkt, allerdings nur einer.

Von diesem Punkt aus geht dann der Strahl los. Das sieht dann so aus:

Dass der Strahl nicht endet, wird dadurch ausgedrückt, dass es keinen Endpunkt gibt.
Auch hier siehst du meistens:

Ein Strahl kann in jede Richtung verlaufen. Es ist davon abhängig, wie du ihn zeichnest. Ein Strahl ist nicht gekrümmt.
Ein Strahl hat einen Anfangspunkt, aber keinen Endpunkt.
Die Länge eines Strahls kannst du nicht messen. Er ist unendlich.
Nicht ganz ernst gemeint: Wenn du einen Strahl ins Heft zeichnest, läuft er unsichtbar immer weiter und weiter. Er schießt ins Weltall!:-)

Der Strahl wird auch Halbgerade genannt.
Die Gerade
Du sagst bestimmt oft das Wort „gerade“.
„Gerade“ verwendest du auf 2 Arten:
- Etwas ist gerade erst passiert. Dann ist es zeitlich gesehen.
- Ein Strich ist gerade. Damit ist gemeint, dass er nicht kurvig oder kruckelig ist.
Die mathematische Gerade
Die Gerade in der Mathematik ist ein Strich ohne Kurven. Die Gerade hat keinen Anfang und kein Ende.
Auf einer Geraden können Punkte liegen. Aber Punkte beginnen oder beenden eine Gerade nicht.
Beispiel für eine Gerade:

Geraden bekommen auch Kleinbuchstaben als Namen.

Auf dieser Geraden liegen die Punkte A und B.

Eine Gerade hat keinen Anfangs- und keinen Endpunkt.
Die Länge einer Geraden kannst du nicht angeben. Die Gerade ist unendlich.
Wenn du in dein Mathematikheft eine Gerade zeichnest, hört die nicht in deinem Heft auf. Sie geht in beide Richtungen bis in das Unendliche weiter. Sie schießt also zweimal ins Weltall. Und das alles ohne Kurven oder Krümmungen.

kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen