Vermischte Aufgaben mit Vierecken
Vierecksarten
Du kennst viele verschiedene Vierecksarten.

Viereck ist nicht gleich Viereck
Jedes Viereck ist eine Ober- oder Unterform von einem anderen Viereck.
Du kannst alle Vierecke in verschiedenen Ebenen in einem Bild einordnen.
Aus einem allgemeinen Viereck kann jedes andere Viereck entstehen. Es ist die Oberform von allen Vierecken und steht ganz oben im Bild.
Das Quadrat ist das speziellste Viereck von allen und somit die Unterform von allen Vierecken. Es steht ganz unten im Bild.
Von oben nach unten siehst du immer die Oberformen und von unten nach oben die Unterformen.
Die Anordnung der Vierecke wird manchmal auch als Haus der Vierecke bezeichnet. Es gibt ein Dach, viele Etagen und ein Fundament.
Alles gleich?
Mit der Anordnung der Vierecke kannst du nun die Beziehungen zwischen verschiedenen Vierecken feststellen.
Wie sieht es zum Beispiel beim Rechteck und rechtwinkligen Trapez aus?

Behauptung: Jedes Rechteck ist ein rechtwinkliges Trapez.
Stimmt die Aussage?
| Rechteck | rechtwinkliges Trapez |
|---|---|
| 4 rechte Winkel | 2 oder 4 rechte Winkel |
2 rechte Winkel haben beide.
Ein Rechteck kann nicht nur zwei rechte Winkel besitzen. Es muss 4 rechte Winkel haben.
Also ist ein Rechteck eine Unterform von einem rechtwinkligen Trapez.
Also ist jedes Rechteck auch ein rechtwinkliges Trapez.
Die Aussage stimmt.
Behauptung: Jedes rechtwinklige Trapez ist ein Rechteck.
Stimmt die Aussage?
1. Möglichkeit: Mit Winkeln begründen
| rechtwinkliges Trapez | Rechteck |
|---|---|
| 2 oder 4 rechte Winkel | 4 rechte Winkel |
Ein rechtwinkliges Trapez kann auch nur zwei rechte Winkel haben.
Ein Rechteck muss 4 rechte Winkel haben.
Also ist das rechtwinklige Trapez eine Oberform von einem Rechteck.
Also kann nicht jedes rechtwinklige Trapez ein Rechteck sein.
Die Aussage ist falsch.
2. Möglichkeit: Mit gleich langen Seiten begründen
| rechtwinkliges Trapez | Rechteck |
|---|---|
| Seiten können unterschiedlich lang sein | sich gegenüberliegende Seiten sind gleich lang |
Die Seiten in einem rechtwinkligen Trapez müssen nicht gleich lang sein.
Die gegenüberliegenden Seiten in einem Rechteck müssen gleich lang sein.
Also ist das rechtwinklige Trapez eine Oberform von einem Rechteck.
Also kann nicht jedes rechtwinklige Trapez ein Rechteck sein.
Die Aussage ist falsch.
Es reicht aus, eine Aussage mithilfe einer Eigenschaft zu überprüfen.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
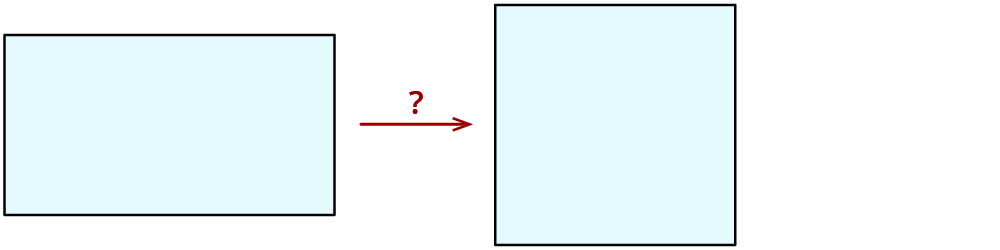
Aus Rechteck mach Quadrat
Mia hat ein rechteckiges Beet.
Sie möchte es in ein quadratisches Beet umwandeln und mit roten Blumen bepflanzen.
Den Rest des Beetes will sie mit Gras zuwachsen lassen.

Was muss Mia verändern, so dass aus dem rechteckigen ein quadratisches Beet wird?
1. Von ihrem rechteckigen Bett misst sie die kürzere Seite.

2. Diese Länge misst sie jeweils auf den längeren Seiten ab. 
3. Danach verbindet sie die Enden der abgesteckten Seiten.
Es entsteht ein Quadrat.

Welche Vierecke sind hier versteckt?
Johann baut mit seinem Bruder Philip aus Legeplättchen ein Boot.
Die Umrisse des Bootes zeichnet Philip auf ein Blatt Papier. 
Ihre Freundin Kiara kommt zum Spielen vorbei. Philip und Johann zeigen ihr das aufgemalte Boot.
Kiara ist begeistert und möchte das Boot nachbauen. Sie überlegt, welche Legeplättchen sie für das Bauen verwenden soll.
Sie sieht:
- ein Quadrat
- ein Rechteck
- ein Parallelogramm
- ein rechtwinkliges Trapez
- eine Raute
Kiara sucht sich die Legeplättchen mit den gefundenen viereckigen Flächen und baut das Boot von den beiden Jungen nach.

kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen