Brüche durch eine natürliche Zahl dividieren
Brüche durch eine natürliche Zahl dividieren
Brüche kannst du nicht nur vervielfachen, sondern auch teilen. Das ist, wenn du deine Kuchenstücke mit anderen teilen musst… :-)
Mathematisch dividierst du dann einen Bruch durch eine natürliche Zahl.
Natürliche Zahlen (ℕ) sind 0, 1, 2, 3, … Das sind die Zahlen, mit denen du abzählst: Schokoriegel, Ferientage, Videos usw.
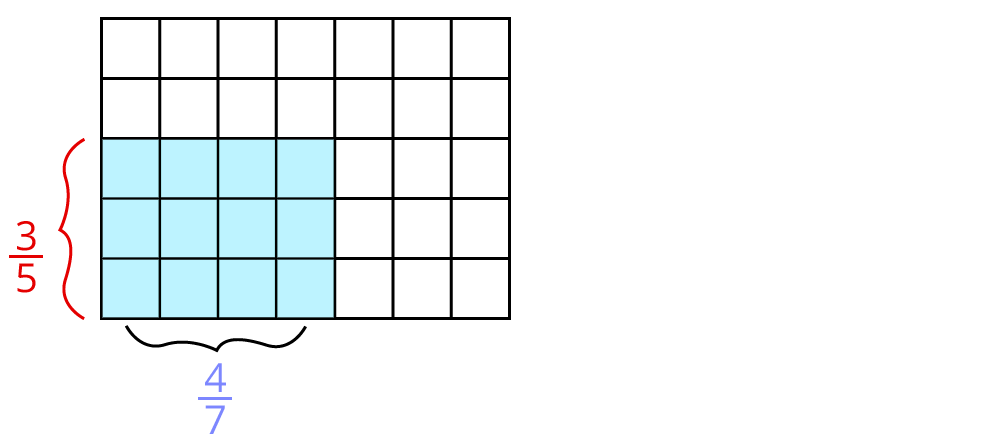
So dividierst du Brüche durch eine natürliche Zahl:
Als Zusammenfassung:
Du dividierst Brüche durch eine natürliche Zahl, indem du den Nenner mit der natürlichen Zahl multiplizierst und den Zähler beibehältst.
Beispiel:
38:5=38·5= 340
Kürzen macht’s einfacher
Oft kannst du kürzen. Beim Dividieren gibt es 2 Möglichkeiten, wann du kürzt.
Beispiel: 47:2
Möglichkeit 1:
Multipliziere den Nenner (in dieser Aufgabe: 7) mit der natürlichen Zahl (in dieser Aufgabe: 2).
47:2=47·2
Hier kannst du schon kürzen:
Im Zähler steht die 4, die du durch 2 teilen kannst; im Nenner steht die 2, die du ebenfalls durch 2 teilen kannst.
47:2=47·2= 27
Möglichkeit 2:
Du rechnest zuerst das Ergebnis aus und kürzt dann.
47:2=47·2=414
Du siehst wegen der Teilbarkeitsregeln, dass 4 und 14 durch 2 teilbar sind. Du kürzt mit 2 und erhältst ebenfalls 27.
47:2=47·2=414=27
Du kannst dir den Weg aussuchen, der dir lieber ist. Aber Kürzen ist Pflicht! :)
Kürzen heißt, dass du eine Zahl aus dem Zähler und eine Zahl aus dem Nenner durch die gleiche Zahl teilst.
Gemischte Zahlen dividieren
Beispiel 1: Bruch als Ergebnis
Berechne 135:2.
- Wandle die gemischte Zahl in einen unechten Bruch um.
So geht’s:
Multipliziere die Ganzen (hier: 1) mit dem Nenner (hier: 5): 1·5= 5
Addiere den bisherigen Zähler (hier: 3): 5+3=8
Behalte den Nenner (hier: 5) bei.
135=85 - Dividiere wie gewohnt. Kürze, wenn möglich.
Multipliziere den Nenner (hier: 5) mit der natürlichen Zahl (hier: 2)
85:2=85·2
Kürze mit 2: Das Ergebnis ist 45. - Wenn möglich, wandle das Ergebnis wieder in eine gemischte Zahl um.
45 ist ein echter Bruch. Den kannst du nicht in eine gemischte Zahl umwandeln.
Alles in einer Rechnung: 135:2=85:2=85·2=45
So dividierst du eine gemischte Zahl durch eine natürliche Zahl:
- Wandle die gemischte Zahl in einen unechten Bruch um.
- Dividiere wie gewohnt. Kürze, wenn möglich.
- Wenn möglich, wandle das Ergebnis wieder in eine gemischte Zahl um.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Gemischte Zahlen dividieren
Beispiel 2: Gemischte Zahl als Ergebnis
Berechne: 523:4.
Wandle die gemischte Zahl in einen unechten Bruch um.
So geht’s:
Multipliziere die Ganzen (5) mit dem Nenner (3): 5·3=15.
Addiere den bisherigen Zähler (2), also 15+2=17.
Behalte den Nenner (3) bei.
523=173Dividiere wie gewohnt. Kürze, wenn möglich.
173:4=173·4=1712
Hier kannst du nicht weiter kürzen.- Wenn möglich, wandle das Ergebnis wieder in eine gemischte Zahl um.
1712=1512
Alles in einer Rechnung: 523:4=173·4=1712=1512
So wandelst du einen Bruch in eine gemischte Zahl um:
- Schreibe den unechten Bruch als Division mit :. Rechne aus.
Oder: Bestimme, wie oft der Nenner in den Zähler passt. - Schreibe den Rest als echten Bruch.
Aller guten Dinge sind drei
Beispiel 3: Mit Kürzen und gemischter Zahl als Ergebnis
Berechne 514:3.
Wandle die gemischte Zahl in einen unechten Bruch um.
514=214Dividiere wie gewohnt. Kürze, wenn möglich.
214:3=214·3
Kürze mit 3: 214·3=74- Wenn möglich, wandle das Ergebnis wieder in eine gemischte Zahl um.
74=134
Alles in einer Rechnung: 514:3=214·3=74=134
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen