Brüche mit einer natürlichen Zahl multiplizieren
Brüche mit natürlichen Zahlen multiplizieren
Du kannst Brüche addieren und subtrahieren (+ und -). Du ahnst es, dann kommt noch die Punktrechnung! Hier kommt erstmal die Multiplikation.
Und wie geht das - einen Bruch vervielfachen? Stell dir das am besten bildlich vor:
Beispiel 1: 14⋅3
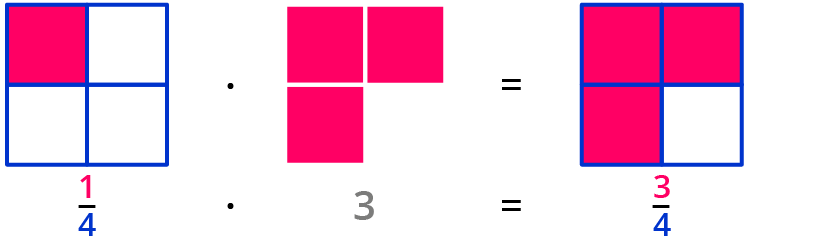
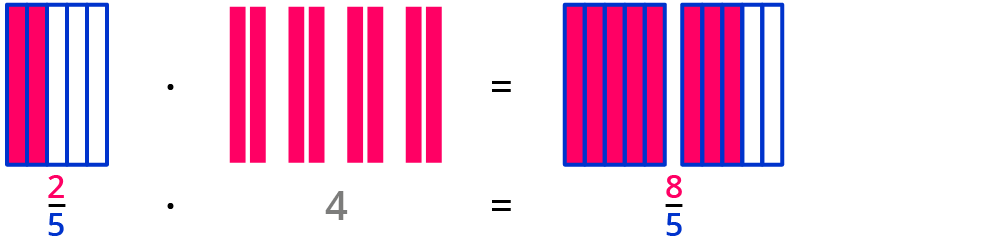
Beispiel 2: 25⋅4 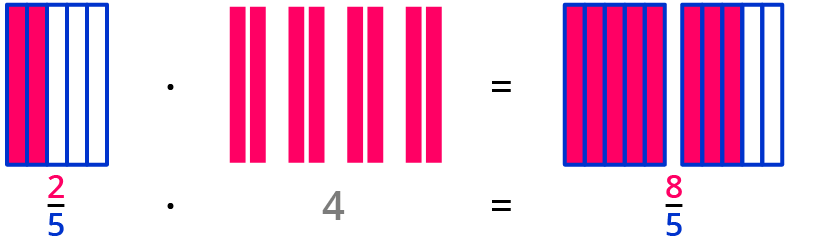
Ein Bruch: ZählerNenner
Die Regel
Wenn du deine Ergebnisse noch einmal zusammenschreibst und farblich markierst, kannst du die Regel für die Multiplikation von Bruch und Zahl selbst erkennen:


Du multiplizierst einen Bruch mit einer ganzen Zahl, indem du den Zähler des Bruches mit der Zahl multiplizierst und den Nenner beibehältst.
Beispiel:
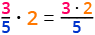
Ergebnisse vereinfachen
Ist dir am Beispiel 25⋅4=85 etwas aufgefallen?
Genau, dieses Ergebnis kannst du vereinfachen!
Hier noch mal das Bild:
Das Ergebnis besteht aus einem Ganzen und noch 35.
Also: 135.
Wenn im Ergebnis einer Multiplikation der Zähler größer als der Nenner ist, kannst du den Bruch in eine gemischte Zahl umwandeln.
Beispiel: 43⋅5=4⋅53=203=623
Vereinfachen durch Kürzen
Erinnerst du dich? Der Wert eines Bruches ändert sich nicht, wenn du den Zähler und den Nenner durch dieselbe Zahl dividierst. Das ist das Kürzen und kommt dir jetzt zugute: Wenn du Brüche multiplizierst, kannst du dir das Rechnen durch geschicktes Kürzen sehr vereinfachen.
Beispiel:
1315⋅5=13⋅515=6515=4515
So weit, so gut. Aber ist die Aufgabe nicht viel einfacher, wenn du erst kürzt?
1315⋅5=13⋅515gekürzt mit 5=13⋅13=133=413
Da kommt etwas anderes heraus? Bedenke, dass du auch 4515 noch mit 5 kürzen kannst: 4515=413.
Und? Welcher Weg war für dich einfacher zu rechnen? Beide Wege sind richtig! Du entscheidest, wie du lieber rechnest.
Wenn du Brüche multiplizierst und geschickt kürzt, kann sich der Rechenweg vereinfachen.
Gemischte Zahlen
Wie rechnest du 235⋅3?
Keine Sorge, das ist einfacher, als du denkst. Ist nur ein Schritt mehr.:-)
Wandle zuerst die gemischte Zahl in einen unechten Bruch um:
235=(2⋅5)+35=10+35=135
Und schon kannst du die Regel anwenden:
135⋅3=13⋅35 (leider kannst du NICHT kürzen) =395
Und vereinfachen:
395=745
Wenn du eine gemischte Zahl mit einer natürlichen Zahl multiplizierst, wandelst du zuerst die gemischte Zahl in einen unechten Bruch um.
Bei einem unechten Bruch ist der Zähler (oben) größer als der Nenner (unten).
Weitere Beispiele
412⋅6=92⋅6=9⋅62=9⋅31=27
3⋅426=3⋅266=3⋅266=1⋅262=262=13
Du kannst die gemischte Zahl auch zerlegen und dann einzeln multiplizieren:
412⋅6=(4+12)⋅6=4⋅6+12⋅6=24+3=27
Es kann sich lohnen, auch mehrfach zu kürzen.
Vergrößern oder verkleinern?
Multiplizierst du eine Zahl mit einem Bruch, dessen Wert größer als 1 ist, vergrößert sich die Zahl:
3⋅43=3⋅43=41=4
Multiplizierst du eine Zahl mit einem Bruch, dessen Wert kleiner als 1 ist, verkleinert sich die Zahl:
5⋅35=5⋅35=31=3
Der Wert eines Bruches richtet sich nach dem Verhältnis aus Zähler und Nenner:
Ist der Zähler GRÖSSER als der Nenner, ist der Wert größer als 1.
Ist der Zähler kleiner als der Nenner, ist der Wert kleiner als 1.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen