Brüche multiplizieren und dividieren
Brüche mit einer Zahl mal nehmen
Das Malnehmen eines Bruches mit einer ganzen Zahl ist das fortgesetzte
+ Rechnen des Bruches.
Beispiel:
3⋅4=3+3+3+3=12
315⋅4=315+315+315+315=1215
In einem Bild sieht das so aus:

Bruch mal Bruch
Bei der Aufgabe 3⋅4=12 kannst du auch alle Zahlen als Brüche aufschreiben:
31⋅41=121
Jetzt kannst du dich fragen, was mit den Zahlen im Nenner passiert ist. Sie werden auch • genommen.
Auch die Aufgabe 315⋅4 kannst du nur mit Brüchen notieren.
315⋅41=1215
Zwei Brüche werden miteinander malgenommen, indem die beiden Zähler und die beiden Nenner miteinander malgenommen werden.
Beispiel:
35⋅47=1235
Mit einem Bild sieht das so aus:
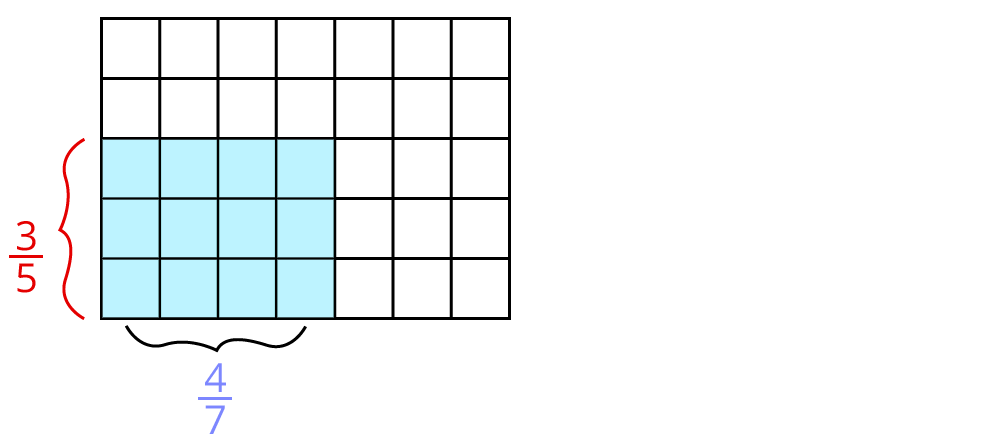
Kürzen vor dem Ausrechnen
Du kannst zwei Brüche beim Malnehmen vor dem Ausrechnen kürzen. Dazu musst du sie auf einem gemeinsamen Bruchstrich aufschreiben. Das ist eine Vereinbarung.
Durch das Kürzen wird das Ausrechnen oft viel einfacher. Die Herausforderung besteht darin, die Kürzungszahl gleich zu sehen.
So kannst du kürzen:
Beispiel 1:
 Gekürzt wurde durch 2.
Gekürzt wurde durch 2.
Beispiel 2:
 Gekürzt wurde durch 3.
Gekürzt wurde durch 3.
Beispiel 3:
 Gekürzt wurde durch 7.
Gekürzt wurde durch 7.
Für die größtmögliche Kürzungszahl suchst du den größten gemeinsamen Teiler der beiden Zahlen (ggT). Es hilft dir auch, wenn du die Teilbarkeits- regeln gut beherrschst.
Beispiel:
Eine Zahl ist durch 9 teilbar, wenn ihre Quersumme durch 9 teilbar ist. Eine Zahl ist durch 5 teilbar, wenn die letzte Ziffer eine 5 oder eine 0 ist.
Regel in Reimform:
„Bruch mal Bruch das ist für Kenner, Zähler mal Zähler und Nenner mal Nenner.“
Kürzen in Bildern:
Hier ist aufgezeichnet, wie Kürzen erlaubt ist. Die gleiche Farbe steht dafür, dass diese beiden Symbole gekürzt wurden.

Mehrmaliges Kürzen vor dem Ausrechnen
Es gibt Aufgaben, da kannst du mehrfach kürzen.
Beispiel:

Du hättest auch anders kürzen können und hättest dasselbe Ergebnis bekommen.

Wenn du nicht vor dem Ausrechnen kürzt, sondern erst im Ergebnis, kommt auch dasselbe heraus. Die Zahlen wären nur größer und vielleicht schwieriger zu bewältigen.

Bruch : Zahl
Stell dir vor, du hast 12 Pizza. Die willst du gerecht auf 2 Personen aufteilen. Jeder bekommt 14 Pizza.
Wenn du 14 Pizza gerecht auf zwei Personen aufteilst, bekommt jeder 18 Pizza.
Mit Zahlen sieht das so aus:
12:2=14
14:2=18
Die Regel ist, dass du die Zahl im Nenner ⋅ rechnest.
Das sieht dann so aus:
12:2=12⋅2=14
14:2=14⋅2=18
Bruch : Bruch
Du kannst die : Beispielaufgaben von eben auch nur mit Brüchen aufschreiben.
12:2=12:21
Wenn du die 2 im Nenner ⋅ nimmst, passiert auch etwas mit der 1. Sie wird im Zähler ⋅ genommen.
Die Regel lautet:
Du teilst durch einen Bruch, indem du mit dem Kehrwert (des zweiten Bruches ) ⋅ nimmst.
Beispiel:
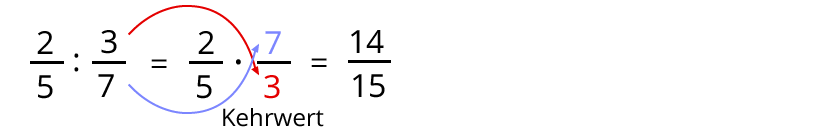
Als Kehrbruch wird der Bruch mit getauschtem Zähler und Nenner bezeichnet.
Beispiel:
Bruch Kehrwert
12 21
: ist die Umkehrung von ⋅
Es gilt weiterhin, dass : Rechnen die Umkehrung von ⋅ Rechnen ist.
Deswegen gilt auch, dass 1215:4=315 ist. Hier kommt die ausführliche Rechnung:
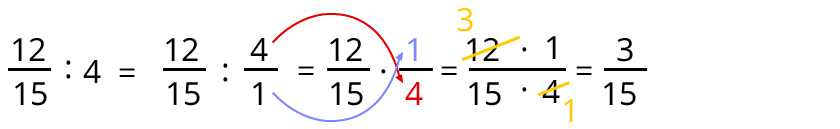
Hier wurde auf dem gemeinsamen
Bruchstrich gekürzt
In einem Bild sieht das so aus:

Zum Vergleich:
315⋅4=315+315+315+315=1215
Kürzen vor dem Ausrechnen
Auch beim : Rechnen kannst du in Aufgaben kürzen, nachdem du sie mit dem Kehrwert aufgeschrieben hast.
Beispiel:
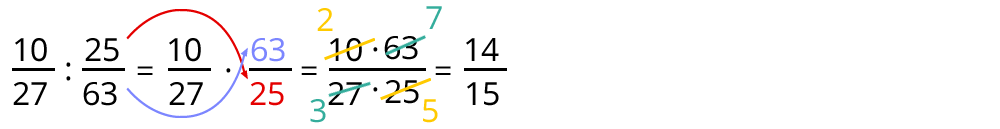
Regel in Reimform:
„Teilst du durch ’ne gebrochene Zahl, nimmst du mit dem Kehrwert mal.“
: und ⋅ Rechnen mit gemischten Zahlen
Vor dem ⋅ und : Rechnen wandelst du gemischte Zahlen immer in unechte Brüche um.
Beispiel:
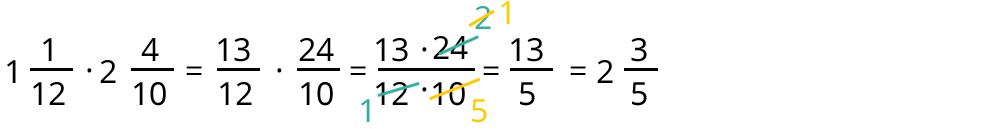
Beispiel für Division
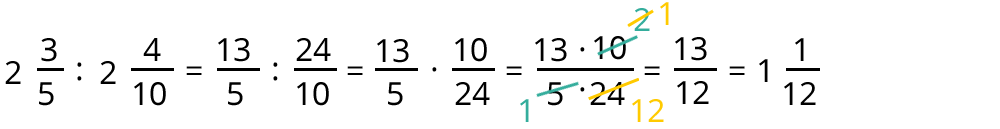
Der letzte Schritt ist hier, die 1312 wieder in die gemischte Schreibweise umzuwandeln.
Der Doppelbruch
Eine andere Art, eine Divisionsaufgabe von Brüchen zu notieren ist der Doppelbruch.
Beispiel:
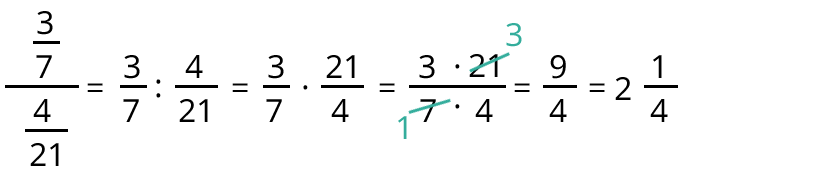
Du schreibst die Doppelbruchaufgabe immer erstmal in einer Reihe auf.
Denk daran, dass der Bruchstrich eines Bruches nichts anderes als : bedeutet.
Das Bruchgedicht
Jetzt kannst du alle Rechenarten mit Brüchen lösen. Es hilft dir, jetzt ein Gedicht auswendig zu lernen:
Willst du Bruch zu Bruch addieren
Bruch von Bruch gar subtrahieren
musst du sie vor allen Dingen
auf den selben Nenner bringen.
Zähler dann zusammenfassen
Nenner unverändert lassen.
Bruch mal Bruch das ist für Kenner
Zähler mal Zähler
Nenner mal Nenner.
Teilst du durch ‘ne gebrochene Zahl
nimmst du mit dem Kehrwert mal.
Und zum Schluss als feine Würze
wenn es möglich ist dann kürze.
Zwei Rechenarten bei Brüchen kombiniert
Wenn du zwei Rechenarten in der Bruchrechnung vorliegen hast, gilt weiter:
- Klammer zuerst berechnen
- Punkt vor Strichrechnung
- Von links nach rechts rechnen
Beispiel:
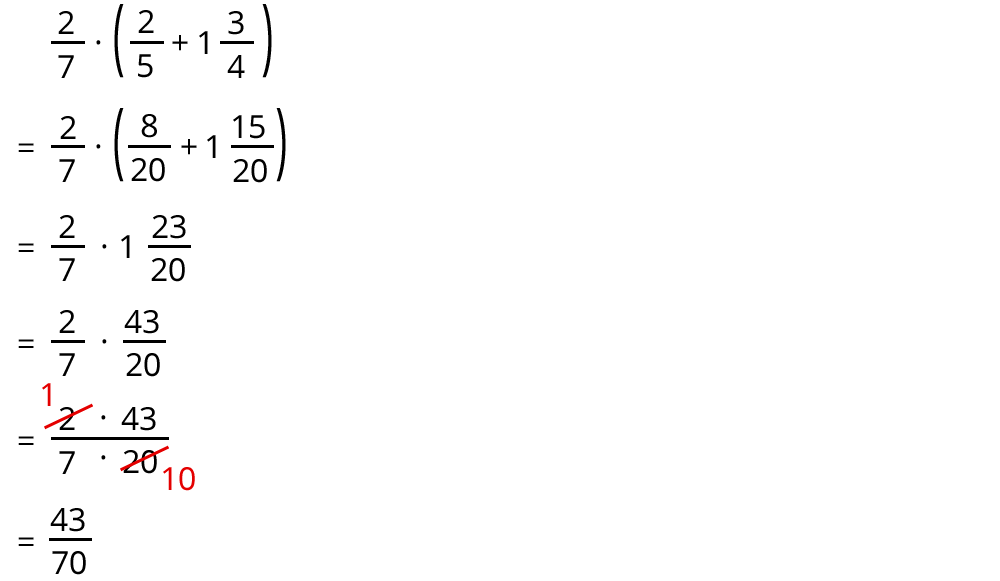
Zwei Zahlschreibweisen kombiniert
Wenn du eine Aufgabe mit Dezimalzahl und Bruchzahl vorliegen hast, kannst du alle Dezimalzahlen in Brüche umwandeln.
Beispiel:
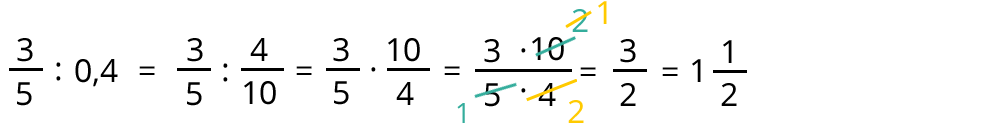
Brüche im Formel-Editor
In kapiert.de gibst du Brüche mit dem Formel-Editor ein. So geht’s:
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen


