Dezimalbrüche multiplizieren und dividieren
Dezimalzahlen und das Multiplizieren und Dividieren mit 10er Zahlen
Das Multiplizieren oder Dividieren mit 10er Zahlen ändert die Ziffernfolge der Zahlen nicht. Die Stellung des Kommas wird geändert.
Beispiele:
0,05⋅1=0,05
0,05⋅10=0,5
0,05⋅100=5
0,05⋅1000=50
Das Komma wird um so viele Stellen nach rechts verschoben, wie die 10er Zahl 0en besitzt.
Beispiele:
0,05:1=0,05
0,05:10=0,005
0,05:100=0,0005
0,05:1000=0,00005
Das Komma wird um so viele Stellen nach links verschoben, wie die 10er Zahl 0en besitzt.
Dadurch kommen im Beispiel immer mehr 0en zwischen dem Komma und der 5.
10er Zahlen sind Zahlen mit einer 1 und verschieden vielen 0en.
Jetzt kannst du dich fragen, was passiert, wenn du 0,05:0,1 rechnest. Das Ergebnis ist 0,5. Die Zahl wird also größer.
Die Erklärung ist gut über die Brüche herzuleiten. 0,05:110 ist dasselbe wie 0,05⋅101.
101 ist der Kehrbruch.
Multiplizieren mit Dezimalzahlen
Das Multiplizieren mit Dezimalzahlen ist deshalb leicht, weil du genauso rechnest, als hätten die gegebenen Zahlen kein Komma enthalten.
Erst, wenn du das Ergebnis der Multiplikation kennst, setzt du das Komma auch in das Ergebnis.
Wo gehört das Komma in die Ergebniszahl?
Du zählst alle Stellen der zwei Faktoren der Aufgabe hinter dem Komma. Genau so viele Nachkommastellen besitzt dein Ergebnis.
Beispiele:
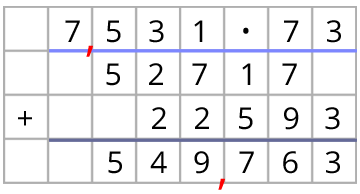 Es gibt drei Nachkommastellen in der ersten Zahl. Dein Ergebnis hat auch drei Nachkommastellen. Es gibt drei Nachkommastellen in der ersten Zahl. Dein Ergebnis hat auch drei Nachkommastellen. | 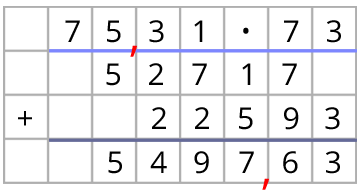 Es gibt zwei Nachkommastellen in der ersten Zahl. Dein Ergebnis hat auch zwei Nachkommastellen. Es gibt zwei Nachkommastellen in der ersten Zahl. Dein Ergebnis hat auch zwei Nachkommastellen. |
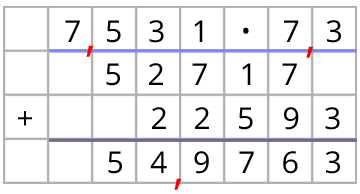 Es gibt drei Nachkommastellen in der ersten Zahl und eine Nachkommastelle in der zweiten Zahl. Dein Ergebnis hat vier Nachkommastellen. Es gibt drei Nachkommastellen in der ersten Zahl und eine Nachkommastelle in der zweiten Zahl. Dein Ergebnis hat vier Nachkommastellen. | 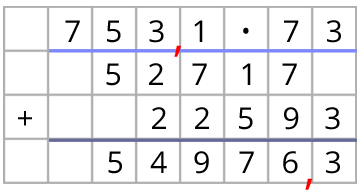 Hier gibt es nur eine Nachkommastelle. Hier gibt es nur eine Nachkommastelle. |
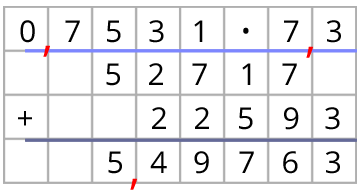 Hier gibt es fünf Nachkommastellen. Hier gibt es fünf Nachkommastellen. |
Wenn du dir unsicher bist, ob du das Komma richtig gesetzt hast, kannst du dein Ergebnis überschlagen.
Beispiel:

Berechne im Kopf 7⋅7=49. Das Ergebnis sollte also etwas größer sein. Du hast das Komma richtig gesetzt.
Division mit Dezimalzahlen
Bei der Division mit Dezimalzahlen gibt es drei verschiedene Fälle für das schriftliche Teilen.
1. In der ersten Zahl steht ein Komma.

Du rechnest, so wie bei der schriftlichen Division bisher. Sobald du das Komma überschreitest (hier steht ein grüner Pfeil), setzt du das Komma im Quotienten. Überschlagen hilft auch hier. Die 15 passt nur einmal in die 28. Also muss hinter der 1 im Ergebnis das Komma gesetzt werden.
Es gibt Aufgaben, in denen du das Komma sofort überschreitest. Im unteren Fall lautet das Ergebnis 0,19.

Die 15 passt auch 0 Mal in die 2 hinein.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Geteiltaufgaben mit Dezimalzahlen
2. Es steht ein Komma in der zweiten Zahl.

Bei diesen Aufgaben wendest du zuerst die Multiplikation mit einer 10er Zahl an, so dass das Komma wegfällt. Du musst beide Zahlen mit der 10er Zahl multiplizieren.
Aus dieser Aufgabe wird 2850:15=.
Jetzt kannst du die Aufgabe wieder wie bekannt lösen.

3. Es stehen in beiden Zahlen Kommas.

Bei diesen Aufgaben verschiebst du das Komma so lange, bis in dem Divisor kein Komma mehr steht. Du wendest wieder die Multiplikation mit 10er Zahlen an. Hier musst du beide Zahlen ⋅10 rechnen. Aus der Aufgabe wird:

Wie du mit dem Komma in der ersten Zahl umgehst, hast du schon im ersten Fall gelernt.
285⋅10=2850
1,5⋅10=15
Dividend : Divisor = Quotient
Die 0 „von oben“ holen
Beim Dividieren kommt es vor, dass du mit den Stellen der Zahl nicht auskommst, um eine Lösung angeben zu können. Du kannst „von oben“ beliebig viele Nullen holen, um die Aufgabe zu lösen.
Beispiel:

Du siehst der Aufgabe nicht an, wie viele 0en du benötigen wirst. Deswegen schreibst du sie nicht gleich in die Aufgabenstellung hinein.
Die Zahl ohne Ende
Durch Division kannst du Zahlen erhalten, die kein Ende nehmen.
Beispiel:

Zahlen wie 1,66666… heißen reinperiodische Zahlen. Du schreibst nicht alle 6en auf, denn es gäbe unendlich viele. Stattdessen schreibst du 1,ˉ6. Der Strich steht immer genau über der Ziffernfolge, die wiederholt wird.
Du kannst die schriftliche Rechnung abbrechen, wenn du siehst, dass du immer denselben Wert beim Subtrahieren erhältst.
Der Spruch „Alles hat ein Ende, nur die Wurst hat zwei.“ , wird von dem Dividieren von Zahlen wiederlegt. Es gibt Zahlen, die nie enden.
Bei der Zahl 3,8756565656… schreibst du 3,87¯56. Hier wiederholen sich die Ziffern 5 und 6. Diese Zahl heißt gemischtperiodisch, weil vor der Periode noch Zahlen stehen, die sich nicht wiederholen.
Periodische Zahlen heißen auch nichtabbrechend.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Noch was Spannendes über Zahlen
Wenn du eine Aufgabe mit :7 rechnest, ist die Periode sehr lang.
1:7=0,¯1428571
2:7=0,¯285714
Du siehst hier, dass sich die Ziffernreihenfolge bei den zwei Divisionsaufgaben wiederholt. Das ist immer so. Würdest du die Ziffernfolge auswendig beherrschen, könntest du das Rechnen nach der ersten Nachkommastelle einstellen. Weitere Ziffern müsstest du dann aus dem Kopf ergänzen. Es kommen immer alle sechs Ziffern beim :7 Rechnen vor.
Wozu brauchst du Dezimalzahlen?
Am häufigsten kommt : und ⋅ mit Dezimalzahlen beim Einkaufen vor.
Beispiel:
Du hast 3,56 € in deinem Portemonnaie. Du möchtest gern Überraschungseier davon kaufen. Ein Ei kostet gerade 0,44 €. Wie viele Eier kannst du kaufen?
Rechnung:
3,56 : 0,44 =
356 : 44 = 8 Rest 4
352
4
Weiter musst du hier nicht rechnen, denn du weißt jetzt, dass du 8 Eier kaufen kannst. Das richtige Ergebnis ist 8,¯09.
Auch wenn du eine Bruchzahl in eine Dezimalzahl umwandeln willst, rechnest du mit Dezimalzahlen.
Beispiel:
25=2:5=0,4
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen