Daten in Klassen einteilen
Eine Mathearbeit von Herrn Wurzel
Mathelehrer Wurzel hat in der 8A (20 Schüler) eine Arbeit schreiben lassen. Es gab maximal 40 Punkte. Das sind die erreichten Punktzahlen:
11 / 12 / 16 / 16 / 19 / 21 / 22 / 23 / 24 / 25
26 / 27 / 27 / 29 / 30 / 31 / 32 / 33 / 37 / 39
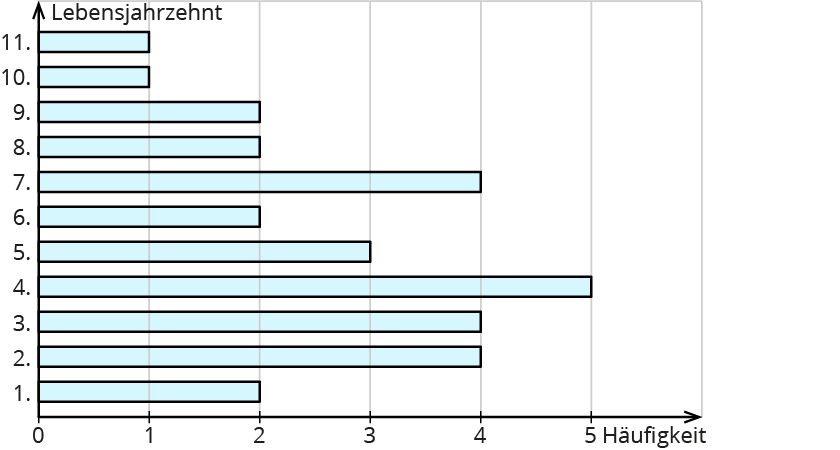
Herr Wurzel erstellt davon ein Säulendiagramm:

Du siehst, dass das nicht gerade übersichtlich ist. Auf der nächsten Seite findet Herr Wurzel eine andere Möglichkeit, einen Überblick über die Punktzahlen zu geben.
Statt eines Säulendiagramms kannst du auch ein Balkendiagramm zeichnen. Die Balken verlaufen dann waagerecht.
Herr Wurzel teilt die Klassen ein
Herr Wurzel legt jetzt fest, bei welchen Punktzahlen es welche Noten gibt. Er legt also Bereiche für die einzelnen Noten fest, z.B. gibt es die Note 1 für 34 bis 40 Punkte.
Mathematiker nennen diese Bereiche auch Klassen.
So hat Herr Wurzel die Noten eingeteilt:
| Punkte | 34 bis 40 | 28 bis unter 34 | 22 bis unter 28 | 16 bis unter 22 | 8 bis unter 16 |
|---|---|---|---|---|---|
| Note | 1 | 2 | 3 | 4 | 5 |
Er kann im nächsten Schritt jede der 20 Arbeiten in die entsprechende Klasse einordnen.
Die Klassen müssen nicht gleich breit sein.
So sind die Noten verteilt
Hier siehst du, wie die 20 Arbeiten den einzelnen Klassen ( Noten ) zugeordnet werden.
| Klasse | 34 bis 40 Note 1 | 28 bis unter 34 Note 2 | 22 bis unter 28 Note 3 | 16 bis unter 22 Note 4 | 8 bis unter 16 Note 5 |
|---|---|---|---|---|---|
| Punkte | 37 39 | 29 / 30 31 / 32 33 | 22 / 23 24 / 25 26 / 27 27 | 16 / 16 19 / 21 | 11 12 |
| Anzahl | 2 | 5 | 7 | 4 | 2 |

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Herr Wurzel zeichnet den Notenspiegel
In der Tabelle hast du gesehen, dass es zum Beispiel 7 Dreien und 5 Zweien gibt. Dazu zeichnet Herr Wurzel ein Säulendiagramm:

Durch die Einteilung von Daten in Klassen werden Diagramme oft viel anschaulicher. Du siehst sofort, wie oft die Noten verteilt wurden.
Allerdings gehen dabei auch Informationen verloren. Du weißt zum Beispiel nicht mehr, welche Punktzahlen die beiden Einser genau hatten.
Durch die Einteilung in Klassen werden Diagramme anschaulicher. Es gehen aber Informationen verloren.
Ceyhan nimmt eine gröbere Einteilung vor
Schülerin Ceyhan hat in der Arbeit 24 Punkte erreicht, also eine Drei geschrieben. Sie teilt die Daten in zwei Klassen ein
- weniger Punkte als sie hat
- mindestens so viele Punkte, wie sie hat
Das Balkendiagramm dazu:

Ceyhan sieht auf einen Blick, ob mehr Schüler besser oder schlechter abgeschnitten haben als sie.
Du siehst: Eine Einteilung in ganz wenige Klassen kann sinnvoll sein. Es gehen aber noch mehr von den vorhandenen Informationen verloren.
Je weniger Klassen es gibt, desto mehr Informationen gehen verloren.
Der Mittelwert bei einer Klasseneinteilung
Hier siehst du nochmal die Einteilung von Lehrer Wurzel:
| Klasse (Note) | 34 bis 40 (1) | 28 bis unter 34 (2) | 22 bis unter 28 (3) | 16 bis unter 22 (4) | 8 bis unter 16 (5) |
|---|---|---|---|---|---|
| Klassenmitte | 37 | 31 | 25 | 19 | 12 |
| Anzahl | 2 | 5 | 7 | 4 | 2 |
Manchmal sollst du aus einer Klasseneinteilung den Mittelwert berechnen. Dazu nimmst du
- die einzelnen Klassenmitten,
- multiplizierst sie mit der jeweiligen Anzahl,
- addierst alles und
- teilst durch die Gesamtzahl der Daten.
Also: 37⋅2+31⋅5+25⋅7+19⋅4+12⋅2=25,2
Der tatsächliche Mittelwert aller 20 Punktzahlen beträgt übrigens 25,0.
Beispiele: Berechnung der Klassenmitte
- 34 - 40: (34+40):2=37
- 16 - unter 22: (16+22):2=19
- 8 - unter 16: (8+16):2=12
Der so errechnete Mittelwert liegt fast immer sehr nah am tatsächlichen Mittelwert.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen