Funktionen als eindeutige Zuordnungen beschreiben
Besondere Zuordnungen: Funktionen
Schon beim Thema Zuordnungen hast du untersucht, wie der Wert einer Größe vom Wert einer anderen Größe abhängt.
Beispiele:
- Der Benzinverbrauch beim Auto hängt von der gefahrenen Strecke ab.
- Die Note einer Arbeit hängt von den erreichten Punkten ab.
Das besondere an Funktionen ist, dass jedem Element einer Ausgangsmenge genau ein Element einer Zielmenge zuordnet wird.
Eine Funktion ist eine eindeutige Zuordnung.
Noch ein Beispiel:
Für einen Teich soll im Schulgarten eine Grube ausgehoben werden. Dabei hängt die Zeit für das Ausheben der Grube von der Anzahl der Schülerinnen und Schüler ab, die helfen.
| Anzahl der Helfer | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Dauer der Arbeit | 240 | 120 | 80 | 60 |
Diese Zuordnung ist eindeutig:
Zu jeder Anzahl von Helfern gibt es genau eine voraussichtliche Dauer der Arbeit. Es handelt sich also um eine Funktion.
Funktionen können in Worten, als Pfeildiagramm, als Wertetabelle oder als Graph dargestellt werden.
Funktionen in Worten
Beispiel:
Jedem Rechteck wird sein Flächeninhalt zugeordnet.
→ Jedes Rechteck hat einen eindeutig bestimmten Flächeninhalt. Es handelt sich also um eine Funktion.
Gegenbeispiel:
Jeder Zahl werden die Vielfachen der Zahl zugeordnet.
→ Da jede Zahl unendlich viele Vielfache hat, ist diese Zuordnung nicht eindeutig und somit keine Funktion.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Funktionen als Pfeildiagramme
Beispiel
…hat die Lieblingsfarbe… 
Jedem Namen wird genau eine Lieblingsfarbe zugeordnet. Es handelt sich also um eine Funktion.
Hinweis: Verschiedenen Namen kann dieselbe Lieblingsfarbe zugeordnet werden. Andreas und Daniel haben die Lieblingsfarbe rot. Entscheidend ist, dass einem Namen nicht mehr als eine Lieblingsfarbe zugeordnet wird.
Gegenbeispiel:
… hat in seinem T-Shirt die Farben … 
Andreas werden zwei Farben zugeordnet. Es handelt sich also nicht um eine Funktion.
Funktionen als Wertetabellen
Beispiel
| Zahl | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Quadrat der Zahl | 1 | 4 | 9 | 16 | 25 |
Jeder Zahl wird das Quadrat der Zahl zugeordnet. Diese Zuordnung ist eindeutig. Es handelt sich also um eine Funktion.
Gegenbeispiel
| Zahl | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Teiler der Zahl | 1 | 1,2 | 1,3 | 1,2,4 |
Jeder Zahl werden die Teiler der Zahl zugeordnet. Da jede Zahl mindestens zwei Teiler hat, ist diese Zuordnung nicht eindeutig und somit keine Funktion.
Funktionen als Graphen
Beispiel:
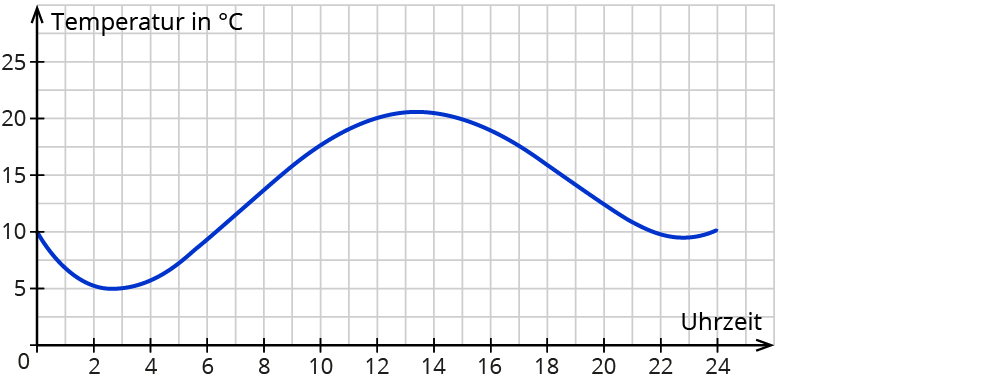
In einer Wetterstation werden laufend die Werte für die Lufttemperatur aufgezeichnet.

Jeder Uhrzeit wird eine Temperatur zugeordnet. Diese Zuordnung ist eindeutig. Es handelt sich also um eine Funktion.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Funktionen als Graphen
Gegenbeispiel

In diesem Graph werden dem x-Wert 0 die y-Werte 3 und -3 zugeordnet.
Diese Zuordnung ist nicht eindeutig und somit keine Funktion.
Der Senkrechten-Test: Schneidet jede Senkrechte zur x-Achse den Graphen einer Zuordnung nur in einem Punkt, dann handelt es sich um eine Funktion.
Schneidet eine Senkrechte den Graphen in 2 oder mehr Punkten, ist es keine Funktion.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen