Entdeckungen am Steigungsdreieck

Das geht noch alles mit dem Steigungsdreieck:

Wenn $$m$$ gar nicht gleich erkennbar ist

Rechnerische Lösung

Das Ergebnis kannst du durch Rechnung bestätigen: Aus den Koordinaten zweier Punkte $$P_1(x_1|y_1)$$ und $$P_2(x_2|y_2)$$ kann man den zugehörigen linearen Funktionsterm berechnen:

1. Die Steigung ist $$m=(y_2-y_1)/(x_2-x_1)={\text{Differenz der }y \text{-Werte}}/{\text{Differenz der }x\text{-Werte}}$$

also $$m=(135-55)/(10-2)=80/8=10$$.

2. Den Achsenabschnitt berechnest du mit einem der beiden Punkte:

$$f(x)=10x+b$$ und $$f(2)=55$$, also
$$10*2+b=55$$
$$20+b=55$$   $$|-20$$
$$b=35$$

Also ergibt sich auch rechnerisch $$y=f(x)=10x+35$$.

Das Steigungsdreieck kann man verschieben

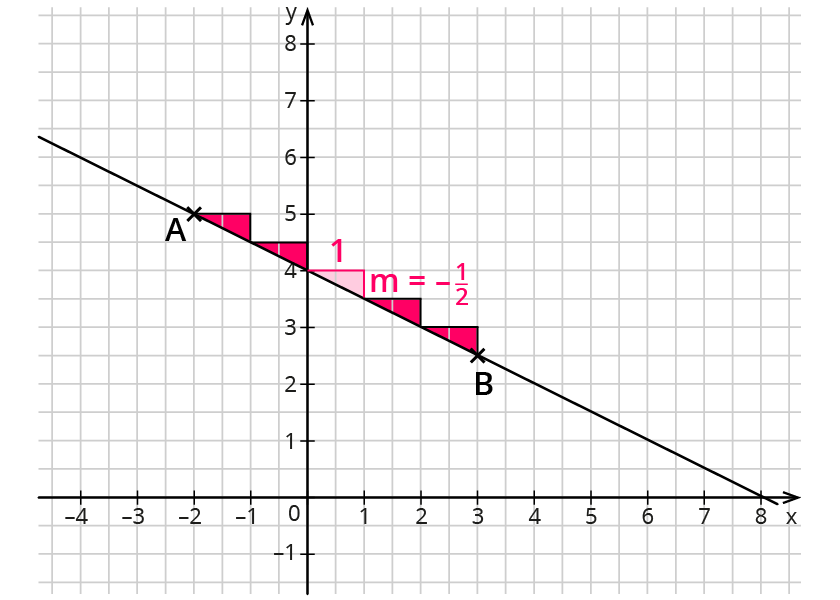
Gegeben sind die beiden Punkte $$A(-2|5)$$ und $$B(3|2,5)$$.

Die Steigung $$m$$ ist die gleichbleibende Änderungsrate.

Nimmt $$x$$ um $$1$$ zu, ändert sich $$y$$ um den Wert der Steigung $$m$$.

Das Steigungsdreieck wiederholt sich an einer beliebigen Stelle der Geraden.

Das Steigungsdreieck kann man vergrößern!

Ändert sich $$x$$ nicht um $$1$$, sondern um einen größeren Wert, muss $$y$$ sich entsprechend um ein Vielfaches von $$m$$ ändern.

$$x$$ wächst von $$-2$$ bis $$3$$, also um $$5$$, $$y$$ muss sich also auch um das 5-fache von $$m$$ ändern, hier also um $$- 2,5$$.

Aus den fünf kleinen Steigungsdreiecken kannst du auch ein großes Steigungsdreieck machen, das die beiden gegebenen Punkte als Eckpunkte enthält.

Die $$x$$-Seite geht dann von $$-2$$ bis $$3$$ nach rechts, die $$y$$-Seite von $$5$$ bis $$2,5$$ nach unten. Die gleichmäßige Änderungsrate $$m$$ ergibt sich dann als Bruch

$$m=(2,5-5)/(3-(-2))=-2,5/5=-1/2$$.

Man kann das Steigungsdreieck beliebig vergrößern, verkleinern oder verschieben.
Wenn man zwei Geradenpunkte hat, kann man vom ersten in $$x$$-Richtung nach rechts gehen, bis man in $$y$$-Richtung zum zweiten Geradenpunkt gelangt.

Die Änderungsrate $$m$$ kann man dann berechnen:

$$m={\text{Differenz der }y \text{-Werte}}/{\text{Differenz der }x\text{-Werte}}$$

Wenn $$m$$ gar nicht gleich erkennbar ist

Eine Wasseruhr zeigt Ende Februar einen Verbrauch von 55 m³ an, Ende Oktober sind es 135 m³.

Zeichne den Graphen und ermittle seine Funktionsgleichung.

Zeichnerische Lösung

Du zeichnest einfach das Steigungsdreieck mit den beiden gegebenen Punkten – du darfst es ja beliebig verschieben und vergrößern.
Jetzt liest du einfach Breite und Höhe des Steigungsdreiecks ab und erhältst $$m=80/8=10$$.

Auch den Achsenabschnitt kannst du ablesen und erhältst $$y=f(x)=10x+35$$.