Lineare Funktionen zeichnen
Lineare Funktionen
Eine Funktion mit der Funktionsgleichung f(x)=mx+b heißt lineare Funktion.
Aus der Funktionsgleichung kannst du ablesen, wie der Graph der Funktion verläuft.
m gibt die Steigung der Geraden an.
b gibt den Schnittpunkt S(0∣b) mit der y-Achse an.
b wird auch als y-Achsenabschnitt bezeichnet.

Der Graph einer linearen Funktion ist eine Gerade
Graphen linearer Funktionen zeichnen
Zeichne den Graphen der Funktion f(x)=0,5x+1.
1. Schritt: Lies in der Funktionsgleichung b ab und trage den Punkt S(0∣b) in das Koordinatensystem ein.
b=1 und S(0∣1)
2. Schritt: Stelle die Steigung m als Bruch dar.
m=0,5=12
3. Schritt: Gehe von dem markierten Punkt nach rechts und nach oben oder unten.
Gehe um 2 nach rechts und um 1 nach oben.
4. Schritt: Lege durch beide Punkte eine Gerade.

Trick bei ganzen Zahlen: 31=3
Übersicht Steigung m


Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Beispiele
1) Für positives m:
Zeichne den Graphen der Funktion f(x)=3x-2.
1. Schritt: Trage den Punkt S(0∣-2) ein.
2. Schritt: 3=31
3. Schritt: Gehe von diesem Punkt aus um 1 nach rechts und um 3 nach oben.
4. Schritt: Lege durch beide Punkte eine Gerade.

m=3 ist positiv, also gehst du um 3 nach oben.
Ist m positiv, so steigt der Graph.
Beispiele
2) Für negatives m:
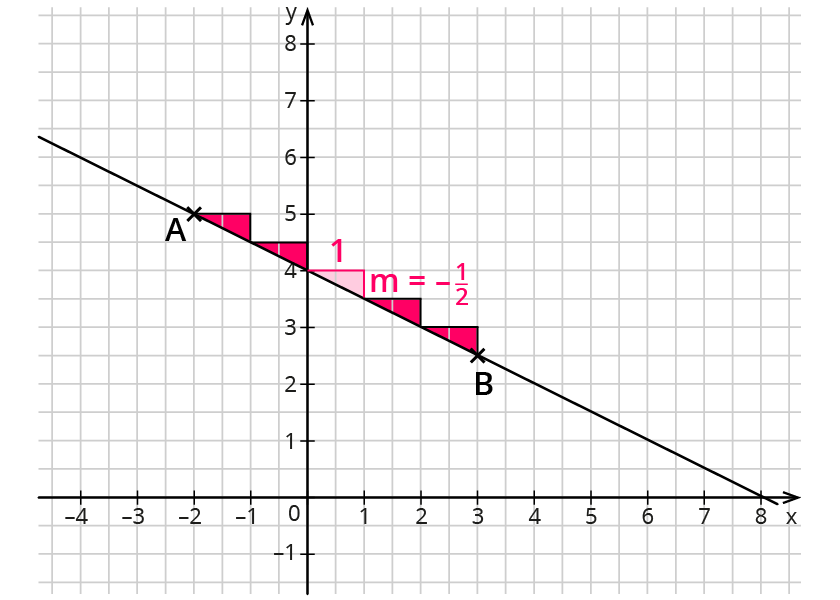
Zeichne den Graphen der Funktion f(x)=-4x+3.
1. Schritt: Trage den Punkt S(0/3) ein.
2. Schritt: -4=-41
3. Schritt: Gehe von diesem Punkt aus um 1 nach rechts und um 4 nach unten.
4. Schritt: Lege durch beide Punkte eine Gerade.

m=-4 ist negativ, also gehst du um 4 nach unten.
Ist m negativ, so fällt der Graph.
Spezialfälle
- Die Geradengleichung lautet: f(x)=mx.
Ausführlich: f(x)=mx+0.
Das heißt b=0. Der Schnittpunkt mit der y-Achse ist S(0∣0).
Beispiel: f(x)=5x

- Die Geradengleichung lautet: f(x)=b.
Ausführlich: f(x)=0⋅x+b.
Das heißt m=0. Der Graph ist eine Parallele zur x-Achse durch den
Punkt S(0∣b).
Beispiel: f(x)=4


Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Zusammenfassung
Zeichne den Graphen der Funktion f(x)=34x+1.
1. Schritt: Trage den Punkt S(0∣1) ein.
2. Schritt: 34 ist schon ein Bruch.
3. Schritt: Gehe von diesem Punkt aus um 4 nach rechts und 3 nach oben.
Nochmal die Übersicht:


So geht’s in kapiert.de
In manchen Aufgaben in kapiert.de kannst du selbst die Graphen einzeichnen! So geht’s:
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen