Gehört zu jeder Geraden eine lineare Funktion?

Du weißt schon, dass zu jeder linearen Funktion eine Gerade als Graph gehört.

Aber gilt das auch umgekehrt, kannst du auch zu jeder Geraden eine Funktionsgleichung finden?

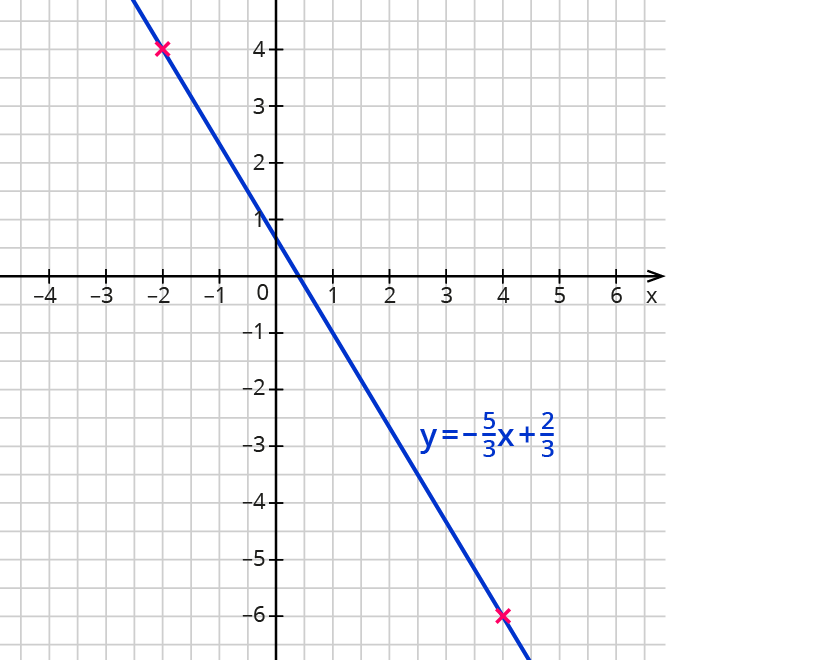
In der Gleichung $$f(x) = mx + b$$ gibt $$m$$ die Steigung und $$b$$ den Abschnitt auf der $$y$$-Achse an.
Die Steigung m gibt an, ob die Gerade nach rechts ansteigt (wenn $$m>0$$ ist) oder abfällt (wenn $$m<0$$ ist)

Wenn die Gerade parallel zu einer der Achsen verläuft, kannst du gar kein Steigungsdreieck einzeichnen, du kannst auch keine gleich bleibende Änderungsrate erkennen – kann es sich trotzdem um eine Funktion handeln?

Die Gerade ist parallel zur $$x$$-Achse – Gleichung $$y=c$$

Hier handelt es sich um Funktionen, denn

1. Alle $$x$$-Werte haben einen $$y$$-Wert, wenn auch immer denselben.
2. Die Zuordnung ist eindeutig, denn kein $$x$$-Wert hat zwei verschieden $$y$$-Werte.

Die $$x$$-Achse besteht aus allen Punkten mit der $$y$$-Koordinate $$0$$, du kann sie also beschreiben mit der Gleichung $$y=0$$. Diese Gleichung beschreibt alle Punkte mit der $$y$$-Koordinate $$0$$ und einem beliebigen $$x$$-Wert, also alle Punkte, die auf der $$x$$-Achse liegen.

Entsprechend kannst du jede Parallele zur x-Achse beschreiben – für die vier Geraden im Bild also $$y=–1$$; $$y=0$$; $$y=1,5$$ und $$y=4$$.

Es gibt einen Achsenabschnitt $$b$$, wie bei allen linearen Funktionen kannst du ihn auf der $$y$$-Achse ablesen, und die Steigung ist weder positiv, noch negativ, sondern es gilt $$m=0$$.

Die Gerade ist parallel zur $$y$$-Achse – Gleichung $$x=c$$

Du siehst schnell, dass diese Zuordnung nicht eindeutig ist, denn ein $$x$$-Wert kann mehrere $$y$$-Werte besitzen. Es handelt sich hierbei also um keine Funktionen (genauer gesagt: keine Funktionen bezüglich der Variablen $$x$$).

Die $$y$$-Achse besteht aus allen Punkten mit der $$x$$-Koordinate $$0$$, du kannst sie also beschreiben mit der Gleichung $$x=0$$. Diese Gleichung beschreibt alle Punkte mit der $$x$$-Koordinate $$0$$ und einem beliebigen $$y$$-Wert, also alle Punkte, die auf der $$y$$-Achse liegen.

Entsprechend kannst du jede Parallele zur $$y$$-Achse beschreiben, für die vier Geraden im Bild also $$x=–1$$; $$x=0$$; $$x=1,5$$ und $$x=4$$.

Da diese Gleichungen aber keiner Funktionsgleichung der Form $$f(x)=mx+b$$ entsprechen, kannst du weder einen Achsenabschnitt $$b$$ noch eine Steigung $$m$$ angeben.