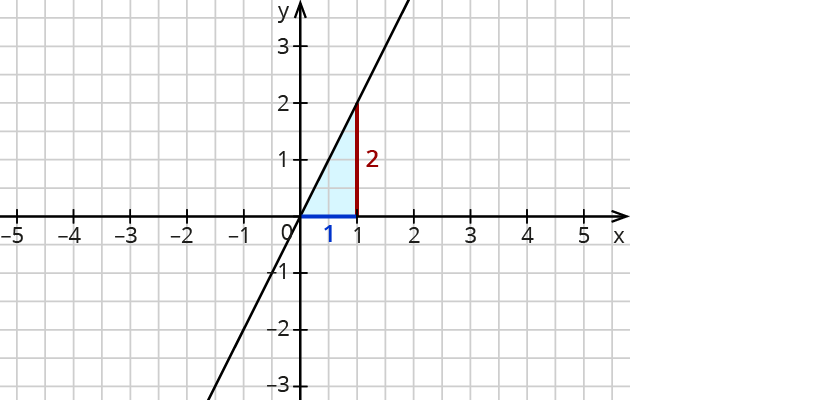
Proportionale Funktionen beschreiben
Proportionale Funktionen
Eine Zuordnung mit der Funktionsgleichung f(x)=mx ist eine proportionale Funktion.
m ist dabei der Proportionalitätsfaktor.
Der Graph einer proportionalen Funktion ist eine Gerade durch den Koordinatenursprung.

Die Definitionsmenge einer proportionalen Funktion sind die Rationalen Zahlen ℚ.
Zuordnungen, bei denen die Verdoppelung des Ausgangswerts („doppelt so viele Eier“) auch zu einer Verdoppelung des zugeordneten Werts („doppelt so viele €“) führt, heißen proportionale Zuordnungen oder Funktionen.
Rationale Zahlen sind positive und negative Brüche.
Wertetabellen zu proportionalen Funktionen erstellen
Lege für die Funktion f(x)=2x eine aussagekräftige Wertetabelle an.
So gehst du vor:
- Schritt:
Überlege dir für welche x-Werte du eine Wertetabelle aufstellen sollst. Ist nichts vorgegeben, so nehme ein paar Werte größer und ein paar Werte kleiner Null
Wähle hier -3,-2,-1,0,1,2,3 als x-Werte. - Schritt: Setze jeden einzelnen x-Wert in die Funktionsgleichung ein und berechne den entsprechenden y-Wert.
y=f( -3 ) =2⋅(-3)=-6
y=f(-2)=2⋅(-2)=-4
y=f(-1)=2⋅(-1)=-2
y=f(0)=2⋅0=0
y=f(1)=2⋅1=2
y=f(2)=2⋅2=4
y=f(3)=2⋅3=6x y - 3 - 6 - 2 - 4 - 1 - 2 0 0 1 2 2 4 3 6
| x | y |
|---|---|
| - 3 | |
| - 2 | |
| - 1 | |
| 0 | |
| 1 | |
| 2 | |
| 3 |
Graph aus einer Wertetabelle zeichnen
Trage die Punkte aus der Wertetabelle in ein Koordinatensystem ein und zeichne den Graphen der Funktion.
| x | y |
|---|---|
| - 3 | - 6 |
| - 2 | - 4 |
| - 1 | - 2 |
| 0 | 0 |
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
Gehe so vor:
- Schritt: Zeichne ein Koordinatensystem und wähle eine günstige Achseneinteilung. Alle Punkte aus der Wertetabelle müssen eingetragen werden können.
Wähle 2 Kästchen als eine Einheit. - Schritt: Trage die Punkte aus der Wertetabelle in das Koordinatensystem ein.
- Schritt: Zeichne durch die Punkte eine Gerade.



Eine Gerade ist schon durch 2 Punkte festgelegt. Wenn du nur den Graphen der proportionalen Funktion einzeichnen sollst, reichen 2 Punkte aus der Wertetabelle.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Funktionsgleichung aus Sachzusammenhang erstellen
Anna möchte im Supermarkt Süßigkeiten kaufen. Für 2 Tüten Süßigkeiten muss Anna 4 € bezahlen.
Gib die Funktionsgleichung für die proportionale Funktion Anzahl an Tüten → Preis (in €) an.
Gehe so vor:
1. Schritt: Überlege, worum es in der Aufgabe geht.
Es geht um Tüten mit Süßigkeiten und deren Preis.
2. Schritt: Entnehme der Aufgabe ein gegebenes Wertepaar.
2 Tüten kosten 4 €.
3. Schritt: Berechne m. Bilde dazu den Quotienten yx=m.
m=42=2
4. Schritt: Setze m in die allgemeine Funktionsgleichung f(x)=mx ein.
f(x)=2x
Die Zuordnungsvorschrift ordnet jedem x genau ein y zu: x → y.
Den Quotienten nennt man auch Proportionalitätsfaktor.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen