Was heißt kongruent?

Beispiel:

Sieh dir die Stoppschilder an. Diese 4 Stoppschilder sind zueinander kongruent.
Sie sind zueinander verschoben, gedreht oder gespiegelt.

Und was ist nicht kongruent?

Beispiel:

Diese Stoppschilder sind nicht kongruent zueinander, weil sie vergrößert oder verkleinert wurden:

Kongruente Dreiecke

Wenn 2 Dreiecke kongruent sind, stimmen bei ihnen alle Seiten und alle Winkel überein.

Wie kannst du schnell prüfen, ob Dreiecke kongruent zueinander sind? Dazu nimmst du einen der vier Kongruenzsätze.

Hier kommt der erste:

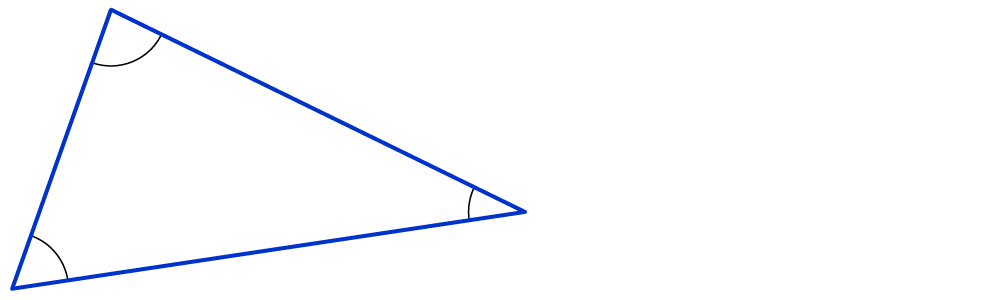
Dabei können die Dreiecke ruhig gedreht oder gespiegelt sein:

SSS anwenden

Beispiel 1:

Dreieck 1:
a = 4,5 cm, b = 3,8 cm, c = 2 cm
Dreieck 2:
a = 4,5 cm, b = 3,8 cm, c = 2 cm

Offensichtlich sind Dreieck 1 und Dreieck 2 jetzt nach dem Kongruenzsatz SSS zueinander kongruent, denn sie stimmen in allen drei Seiten überein.

Beispiel 2:

Dreieck 3:
a = 4,5 cm, b = 3,8 cm, c = 2 cm
Dreieck 4:
a = 2 cm, b = 4,5 cm, c = 3,8 cm

Auch Dreieck 3 und Dreieck 4 sind jetzt nach dem Kongruenzsatz SSS zueinander kongruent. Sie stimmen in allen drei Seiten überein. Allerdings entspricht hier die Seite a von Dreieck 3 der Seite b von Dreieck 4, die Seite b von Dreieck 3 der Seite c von Dreieck 4 usw. Die Reihenfolge der Seiten ist aber noch gleich.

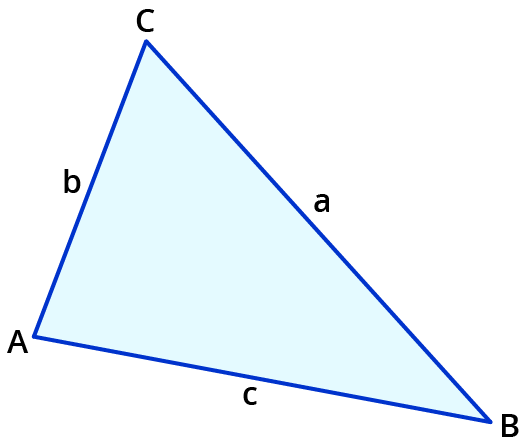
SSS anwenden

Beispiel 3:

Dreieck 5:
a = 4,5 cm, b = 3,8 cm, c = 2 cm
Dreieck 6:
a = 4.5 cm, b = 2 cm, c = 3,8 cm

Nun sind nur die Seiten b und c in ihren Größen vertauscht, der Satz aber dennoch anwendbar, die Dreiecke 5 und 6 also immer noch kongruent, allerdings gespiegelt.

Beispiel 4:

Dreieck 7:
a = 4,5 cm, b = 3,8 cm, c = 2,1 cm
Dreieck 8:
a = 4,5 cm, b = 2 cm, c = 3,8 cm

Seite c von Dreieck 7 hat keine Entsprechung bei Dreieck 8, der Kongruenzsatz ist nicht anwendbar und die beiden Dreiecke demzufolge nicht kongruent zueinander.

Konstruieren mit dem Kongruenzsatz SSS

Ein Dreieck ist genau bestimmt, wenn alle 3 Seiten gegeben sind. Das heißt, du kannst es mit Zirkel und Lineal konstruieren.

Im Folgenden sollst du ein Dreieck mit den Seitenlängen a = 5 cm, b = 3 cm und c = 7 cm konstruieren. Dazu gehst du folgendermaßen vor.

1. Schritt:

Zeichne die Seite c mit den Eckpunkten A und B waagerecht.

2. Schritt:

Zeichne um den Punkt A einen Kreis $$K_1$$ mit dem Radius b.

3. Schritt:

Zeichne um den Punkt B einen Kreis $$K_2$$ mit dem Radius a.

4. Schritt.:

Den oberhalb der Seite c gelegenen Schnittpunkt der beiden Kreise $$K_1$$ und $$K_2$$ bezeichne mit C.

5. Schritt:

Verbinde die Punkte A und C zur Strecke b und B und C zur Strecke a und vervollständige dadurch das Dreieck.

Hinweis: Hättest du in Schritt 4 den unteren und nicht den oberen Schnittpunkt gewählt, hättest Du zwar ein kongruentes Dreieck erhalten, die Reihenfolge der Punkte gegen den Uhrzeigersinn wäre aber nicht mehr korrekt gewesen.

Beweis des Kongruenzsatzes SSS

Was ist eigentlich ein Satz?

In der Mathematik versteht man unter einem Satz eine Aussage, die immer gültig ist. Für jeden Satz gibt es mindestens einen Beweis. Der Beweis zeigt allgemein, dass die Aussage immer gültig ist.

Beispiel:

„Die Summe der Innenwinkel in einem Dreieck ist immer 180°. “

Das ist der sogenannte Innenwinkelsummensatz.

Strenggenommen musst du den Kongruenzsatz SSS auch erst beweisen, um dich zu überzeugen, dass er auch wirklich gültig ist. So würde jedenfalls ein echter Mathematiker vorgehen.:-)

Der Beweis

Du gehst von einem beliebigen Dreieck mit den Seiten a, b und c aus. Startest du mit der Seite c, so gibt es nur zwei Dreiecke: Die Schnittpunkt der beiden Kreise sind oben oder unten. Die stimmen in allen drei Längen überein. Diese beiden Dreiecke sind kongruent zueinander, da sie nur gespiegelt wurden.