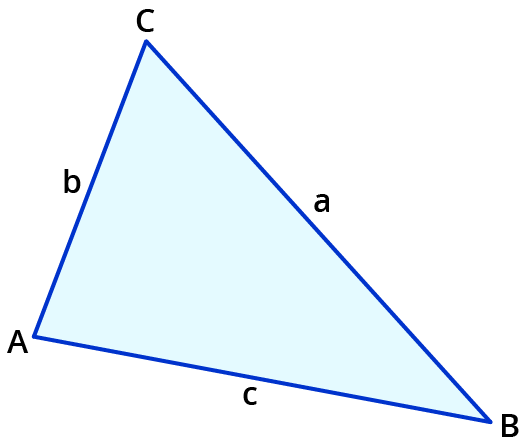
Den Kongruenzsatz SsW nutzen
Der Kongruenzsatz SsW
Du kennst bereits den Kongruenzsatz SWS. Du wendest ihn an, wenn der Winkel von den beiden Seiten eingeschlossen ist. (Deshalb steht das W zwischen den zwei S.)
Der Satz SsW ist so ähnlich: 2 Seiten sind gegeben und der Winkel liegt der längeren Seite gegenüber. Das heißt, eine Seite ist kürzer und wird mit kleinem s geschrieben in SsW.
Kongruenzsatz SsW
Stimmen zwei Dreiecke in zwei ihrer Seiten (Ss) und dem der längeren Seite gegenüberliegenden Winkel (W) überein, so sind sie kongruent zueinander.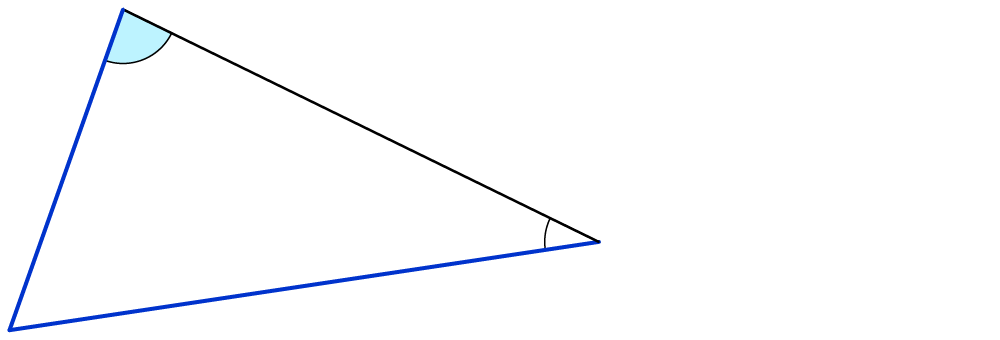
Damit ist der Kongruenzsatz SsW in den folgenden Fällen anwendbar:
1. gegeben: a, b, α, falls a länger ist als b

2. gegeben: a, b, β, falls b länger ist als a

3. gegeben: a, c, α, falls a länger ist als c

4. gegeben: a, c, γ, falls c länger ist als a

5. gegeben: b, c, β, falls b länger ist als c

6. gegeben: b, c, γ, falls c länger ist als b

Anmerkung
Dass du einen Kongruenzsatz nicht anwenden kannst, bedeutet nicht unbedingt, dass die beiden Dreiecke nicht kongruent sind. Es heißt nur, dass du gegebenenfalls ein anderes Argument überlegen musst.
Beispiele
Beispiel 1:
Dreieck 1: a = 4,5 cm, b = 3,8 cm, α = 57°
Dreieck 2: a = 4,5 cm, b = 3,8 cm, α = 57°
Offensichtlich sind Dreieck 1 und Dreieck 2 jetzt nach dem Kongruenzsatz SsW zueinander kongruent, denn sie stimmen in den zwei Seiten a und b und dem der größeren Seite, nämlich a, gegenüberliegenden Winkel α überein.
Beispiel 2:
Dreieck 3: a = 4,5 cm, b = 3,8 cm, α = 57°
Dreieck 4: b = 4,5 cm, c = 3,8 cm, β = 57°
Auch die Dreiecke 3 und 4 sind nach dem Kongruenzsatz SsW zueinander kongruent, denn sie stimmen in zwei Seiten und dem der größeren Seite gegenüberliegenden Winkel überein.
Beispiel 3:
Dreieck 5: a = 4,5 cm, b = 3,8 cm, α = 57°
Dreieck 6: b = 3,8 cm, c = 4,5 cm, γ = 57°
Immer noch lässt sich der Kongruenzsatz SsW anwenden, da die Dreiecke 5 und 6 in zwei Seiten und dem der größeren Seite gegenüberliegenden Winkel übereinstimmen.
Beispiel 4:
Dreieck 7: a = 4,5 cm, b = 3,8 cm, α = 57°
Dreieck 8: b = 4,5 cm, c = 3,8 cm, β = 43°
Für die Dreiecke 7 und 8 lässt sich der Kongruenzsatz SsW nicht anwenden, da die beiden den größeren Seiten gegenüberliegenden Winkel nicht übereinstimmen.
Beispiel 5:
Dreieck 9: a = 4,5 cm, b = 3,8 cm, β = 57°
Dreieck 10: b = 4,5 cm, c = 3,8 cm, β = 57°
Auch hier kann der Kongruenzsatz SsW nicht angewendet werden, da beim Dreieck 9 der Winkel β der kürzeren Seite, nämlich b gegenüberliegt, und nicht der längeren, nämlich a.
Konstruieren mit dem Kongruenzsatz SsW
Mit SsW konstruierst du so:
Konstruktionsbeschreibung
Konstruiere ein Dreieck mit den Seitenlängen a=5 cm, b = 3 cm und dem Winkel α = 50°. Dazu gehst Du folgendermaßen vor.
1. Schritt:
Zeichne die (kürzere) Seite b mit den Eckpunkten A und C.

2. Schritt:
Trage am Punkt A den Winkel α (im Uhrzeigersinn) ab und zeichne durch A die Gerade g.

3. Schritt:
Zeichne um den Punkt C einen Kreis K mit dem Radius a.

4. Schritt.:
Bezeichne den (richtigen) Schnittpunkt der Geraden g mit dem Kreis K mit B.

5. Schritt:
Verbinde die Punkte A und B zur Strecke c.

6. Schritt:
Verbinde die Punkte C und B zur Strecke a.


Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Allgemeines Vorgehen
Um die Konstruktion auch in den anderen Fällen durchführen zu können, gehst du folgendermaßen vor:
| geg. | Schritt 1 (kürzere Seite) | Schritt 2 | Schritt 3 | Schritt 4 | Schritt 5/6 |
|---|---|---|---|---|---|
| a, b, α | b zeichnen | α an A abtragen | Kreis um C mit Radius a | Schnitt- punkt B | a und c zeichnen |
| a, b, β | a zeichnen | β an B abtragen | Kreis um C mit Radius b | Schnitt- punkt A | b und c zeichnen |
| a, c, α | c zeichnen | α an A abtragen | Kreis um B mit Radius a | Schnitt- punkt C | a und b zeichnen |
| a, c, γ | a zeichnen | γ an C abtragen | Kreis um B mit Radius c | Schnitt- punkt A | b und c zeichnen |
| b, c, β | c zeichnen | β an B abtragen | Kreis um A mit Radius b | Schnitt- punkt C | a und b zeichnen |
| b, c, γ | b zeichnen | γ an C abtragen | Kreis um A mit Radius c | Schnitt- punkt B | a und c zeichnen |
Beweis des Kongruenzsatzes SsW
Wenn du dir die Konstruktion näher anschaust, so gab es in der Tat zwei Schnittpunkte zwischen der Geraden g und dem Kreis K. Hättest du dich für den anderen Punkt als Schnittpunkt entschieden, wäre der Winkel bei dem Punkt A nicht mehr 50°, sondern 180°-50° = 130°. Außerdem hätten die Punkte nicht mehr die richtige Reihenfolge.
Das andere Dreieck wäre dann auch keine Spiegelung des richtigen Dreiecks mehr (nur wenn der Winkel zufällig 90° betrüge, wäre das der Fall.) Das heißt, es gibt wirklich nur genau ein Dreieck, das bei der Konstruktion mit SsW entsteht.


kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen