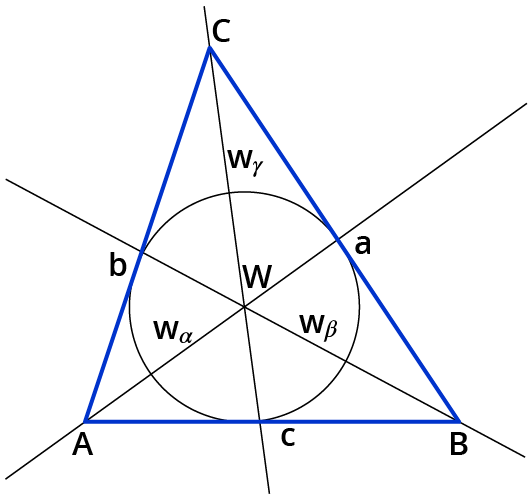
Dreiecksarten kennen
Was ist eigentlich ein Dreieck?
Ein Dreieck besteht aus drei Punkten, die nicht auf einer Geraden liegen und den Verbindungsstrecken.
Die Punkte werden als Ecken und die Strecken als Seiten bezeichnet.
Ein Dreieck besteht also aus drei Ecken und drei Seiten.

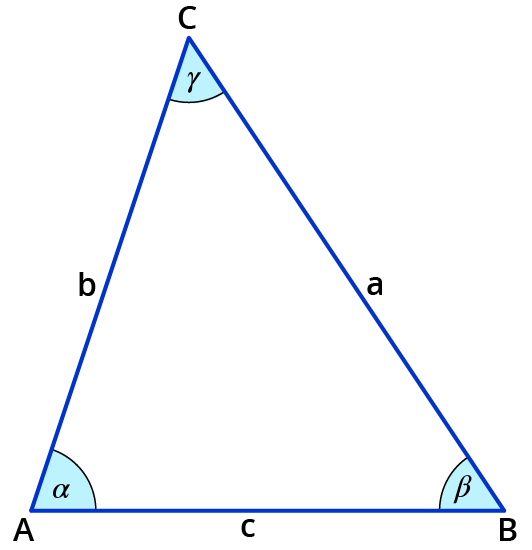
So wird ein Dreieck bezeichnet
Die Ecken werden mit Großbuchstaben (meist A, B und C) bezeichnet.
Die Seiten werden mit Kleinbuchstaben (a, b und c) bezeichnet.
Die Innenwinkel werden mit kleinen griechischen Buchstaben
(α, β und γ) bezeichnet.
Zur Übersicht:
| Eckpunkt | gegenüber- liegende Seite | Innenwinkel |
|---|---|---|
A | α | |
B | β | |
C | γ |
Die Winkelsumme in einem Dreieck
Die Summe der Innenwinkelgrößen in einem Dreieck beträgt immer 180°.
α+β+γ=180°

Auf dem Bild ist α genauso groß wie α1. Das Gleiche gilt für β und β1.
Legst du alle Winkel nebeneinander, so erhältst du einen gestreckten Winkel. Ein gestreckter Winkel ist 180° groß.
Addierst du die Winkelgrößen von α, β und γ, so erhältst du als Ergebnis die Summe von 180°.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Wozu brauchst du die Winkelsumme?
Sind zum Beispiel zwei Winkelgrößen gegeben, kann man recht schnell den dritten fehlenden Winkel berechnen.
geg.: α=55° und β=45°
ges.: γ
α+β+γ=180°
55°+45°+γ=180°
100°+γ=180°
γ=80°
Die Abkürzung geg. heißt gegeben und bedeutet, dass diese Angabe vorhanden ist.
Die Abkürzung ges. heißt gesucht und bedeutet, dass diese Angabe fehlt und berechnet werden soll.
Da gibt es aber noch die Außenwinkel
Die Nebenwinkel der Innenwinkel eines Dreiecks heißen Außenwinkel.
Ein Innenwinkel und der dazugehörige Nebenwinkel ergänzen sich zu 180°.
Die Summe der Außenwinkelgrößen eines Dreiecks beträgt immer 360°.
α´+β´+γ´=360°

Wozu brauchst du die Nebenwinkel?
Ist ein Innenwinkel und ein anderer Nebenwinkel gegeben, kannst du die fehlenden Winkel berechnen.
geg: α´=80° und β=45° ges: α,γ
Du berechnest zuerst den Winkel α:
α+α´=180°
α+80°=180°
α=100°
Dann verwendest du den Satz über die Innenwinkelsumme und berechnest damit γ.
α+β+γ=180°
100°+45°+γ=180°
145°+γ=180°
γ=35°


Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
So werden die Dreiecke eingeteilt Teil 1
Die Dreiecke können nach den Winkelgrößen und nach den Seitenlängen eingeteilt werden.
Einteilung nach Winkelgrößen:
| Art des Dreiecks | Besonderheit |
|---|---|
spitzwinklig  | alle Winkel sind spitz, also: α,β,γ<90° |
rechtwinklig | ein Winkel ist genau 90° groß und die beiden anderen sind spitz, also z.B.: α=90° und β,γ<90° |
stumpfwinklig  | ein Winkel ist stumpf und die beiden anderen sind spitz, also z.B.: α>90° und β,γ<90° |
So werden die Dreiecke eingeteilt Teil 2
Einteilung nach Seitenlängen:
| Art des Dreiecks | Besonderheit |
|---|---|
ungleichseitig | alle Seiten sind unterschiedlich lang, also: a≠b≠c |
gleichschenklig | zwei Seiten sind gleich lang also z.B.: a=b,c≠a und c≠b |
gleichseitig  | alle Seiten sind gleich lang, also: a=b=c |
Wann entsteht ein Dreieck?
Du kannst prüfen, ob 3 gegebene Seitenlängen ein Dreieck ergeben. Und das ohne zu zeichnen!
Das geht mit der Dreiecksungleichung.
Dreiecksungleichung
In einem Dreieck gilt: Addierst du die Länge von zwei Seiten eines Dreiecks, ist das Ergebnis größer als die Länge der dritten Seite.
a+b>c und a+c>b und b+c>a
So gehst du vor:
Du setzt statt den Buchstaben die vorgegebenen Seitenlängen ein und überprüfst, ob die Ungleichungen stimmen oder nicht.
Beispiel 1:
geg: a=3 cm,b=4 cm und c=5 cm
a+b>c⇒3 cm+4 cm>5 cm⇒7 cm>5 cm, das stimmt
a+c>b⇒3 cm+5 cm>4 cm⇒8 cm>4 cm, das stimmt
b+c>a⇒4 cm+5 cm>3 cm⇒9 cm>3 cm, das stimmt
Alle drei Gleichungen sind wahre Aussagen. Das heißt, dass die 3 Seitenlängen a, b und c ein Dreieck ergeben.
Beispiel 2:
geg: a=4 cm,b=2 cm und c=1 cm
a+b>c⇒4 cm+2 cm>1 cm⇒6 cm>1 cm, das stimmt
a+c>b⇒4 cm+1 cm>2 cm⇒5 cm>2 cm, das stimmt
b+c>a⇒2 cm+1 cm>4 cm⇒3 cm>4 cm, das stimmt nicht
Nicht alle drei Gleichungen sind wahre Aussagen. Das heißt, die 3 Seitenlängen a, b und c ergeben kein Dreieck.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Änderungen am Dreieck
Verändere die Figuren
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen