Was ist eine Mittelsenkrechte?

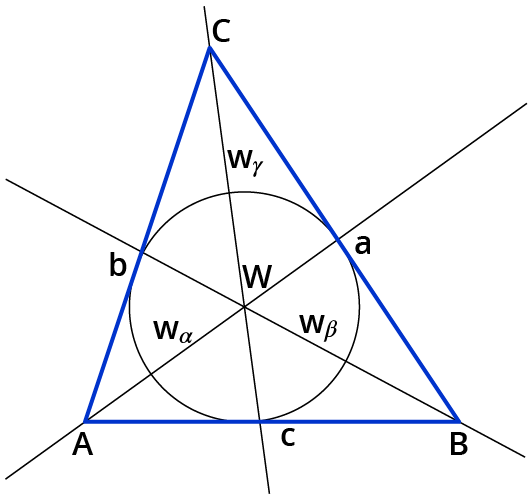
Die Mittelsenkrechten

• gehen durch den Mittelpunkt einer Seite.
• stehen senkrecht auf einer Seite.
• schneiden sich im Punkt M.
  
  

Der Punkt M ist der Mittelpunkt des Umkreises eines Dreiecks.

Was ist der Umkreis eines Dreiecks?

Der Punkt M ist von den Eckpunkten A, B und C eines Dreiecks gleich weit entfernt.
Das heißt, dass die Eckpunkte A, B und C auf einem Kreis mit dem Punkt M als Mittelpunkt liegen.

Dieser Kreis, auf dem alle drei Eckpunkte liegen, heißt Umkreis des Dreiecks.

Wozu ist der Umkreis nützlich?

Im Garten von Tante Waldtraud stehen 3 Baumstümpfe um eine Feuerschale. David, Ömer und Pablo wollen Samstagabend am Feuer sitzen. Sie wollen die Feuerschale so hinstellen, dass sie von den 3 Baumstümpfen genau gleich weit entfernt ist.

Wo genau muss die Feuerschale hin? Wo stehen weitere Baumstümpfe, wenn noch mehr Freunde kommen?

Für diese Aufgabe konstruierst du die Mittelsenkrechten und dann den Umkreis. Auf den folgenden Seiten siehst du, wie es geht.

So ist die Konstruktion der Mittelsenkrechte $$m_a$$ ganz schnell gemacht

1. Schritt:
Stich mit der Zirkelspitze in den Eckpunkt B ein.
Zeichne einen halben Kreisbogen mit einer Zirkelspanne, die größer als die Hälfte der Länge der Seite a ist um B.



2. Schritt:
Stich mit der Zirkelspitze in den Eckpunkt C ein.
Zeichne einen halben Kreisbogen mit der gleichen Zirkelspanne aus dem 1. Schritt um C.
Du erhältst zwei Schnittpunkte der Kreisbögen.



3. Schritt:
Verbinde die Schnittpunkte mit einem Lineal.
Du hast die Mittelsenkrechte der Seite a konstruiert.
Bezeichne sie mit $$m_a$$.

Hier sind die Schritte für eine Strecke noch einmal interaktiv:

Die Mittelsenkrechte $$m_b$$ ist noch schneller fertig

1. Schritt:
Stich mit der Zirkelspitze in den Eckpunkt C ein.
Zeichne einen halben Kreisbogen mit einer Zirkelspanne, die größer als die Hälfte der Länge der Seite b ist um C.



2. Schritt:
Stich mit der Zirkelspitze in den Eckpunkt A ein.
Zeichne einen halben Kreisbogen mit der gleichen Zirkelspanne aus dem 1. Schritt um A.
Du erhältst zwei Schnittpunkte der Kreisbögen.



3. Schritt:
Verbinde die Schnittpunkte mit einem Lineal.
Du hast die Mittelsenkrechte der Seite b konstruiert.
Bezeichne sie mit $$m_b$$.

Die Konstruktion der Mittelsenkrechten $$m_c$$ machst du mit links

1. Schritt:
Stich mit der Zirkelspitze in den Eckpunkt B ein.
Zeichne einen halben Kreisbogen mit einer Zirkelspanne, die größer als die Hälfte der Länge der Seite c ist um B.



2. Schritt:
Stich mit der Zirkelspitze in den Eckpunkt A ein.
Zeichne einen halben Kreisbogen mit der gleichen Zirkelspanne aus dem 1. Schritt um A.
Du erhältst zwei Schnittpunkte der Kreisbögen.



3. Schritt:
Verbinde die Schnittpunkte mit einem Lineal.
Du hast die Mittelsenkrechte der Seite c konstruiert.
Bezeichne sie mit $$m_c$$.

Zu guter Letzt: Konstruiere den Umkreis

1. Schritt:
Konstruiere alle Mittelsenkrechten des Dreiecks.
Du erhältst einen Schnittpunkt aller Mittelsenkrechten.
Bezeichne den Schnittpunkt mit M.



2. Schritt:
Stich mit der Zirkelspitze in den Punkt M ein.

Nimm als Zirkelspanne den Abstand zwischen dem Punkt M und dem Eckpunkt A.

Zeichne um M herum einen vollständigen Kreis.

Alle Eckpunkte liegen auf der Kreislinie.
Du hast den Umkreises eines Dreiecks konstruiert.