Oberfläche eines Prismas berechnen
Was ist die Oberfläche eines Prismas?
Die Oberfläche eines Prismas besteht aus allen äußeren Flächen. Wenn du das Prisma zu einem Netz ausklappst, kannst du alle Flächen gut erkennen:

Du siehst die Mantelfläche und zweimal die Grundfläche.
- Berechne die Grundfläche.
- Berechne die Mantelfläche.
- Berechne:
Oberfläche = 2 ⋅ Grundfläche + Mantelfläche
Kurzschreibweise: O=2⋅G+M
Die äußeren Flächen sind die Flächen, die du berühren kannst, wenn du das Prisma in der Hand hältst.
Wie berechnest du die Grundfläche des Dreiecksprimas?
Gegeben ist ein Dreiecksprisma mit den Kantenlängen
a=4 cm, b=2 cm, c=5 cm,
ha=1,7 cm, hk=3 cm.

Du kannst zweimal die Grundfläche G sehen und die Mantelfläche M, die hier aus drei Rechtecken besteht.
Berechne die Grundfläche so: G=12⋅g⋅h
Da die Dreieckshöhe ha gegeben ist, nimmst du die Seite a als Grundseite g.
G=12⋅a⋅ha
G=12⋅4 cm ⋅ 1,7 cm
G=12⋅6,8 cm2
G=3,4 cm2
ha bezeichnet die Höhe des Dreiecks mit der Grundseite a.
Flächeninhalt eines Dreiecks: A=12⋅g⋅h
- g Grundseite
- h Höhe des Dreiecks

Höhe der Grundfläche ha≠ Höhe des Körpers hk
Wie berechnest du die Mantelfläche des Dreiecksprismas?
Die Mantelfläche besteht aus drei Rechtecken:

Weg 1: Alle einzelnen Rechtecke berechnen
M=a⋅hk+b⋅hk+c⋅hk
M=4 cm ⋅ 3 cm + 2 cm ⋅3 cm + 5 cm ⋅ 3 cm
M=12 cm2 + 6 cm2 + 15 cm2
M=33 cm 2
Weg 2: So geht’s schneller
Die drei Rechtecke kannst du zu einem Rechteck zusammenfassen. Es hat die Seitenlängen:
Körperhöhe des Prismas hk und Umfang u der Grundfläche.
M=hk⋅u
M=11 cm ⋅ 3 cm
M=33 cm 2
Dann ergibt sich für die Oberfläche:
Oberfläche = 2 ⋅ Grundfläche + Mantelfläche
O=2⋅G+M
O=2⋅3,4 cm2 + 33 cm2
O=6,8 cm2 + 33 cm2
O=39,8 cm2
Flächeninhalt eines Rechtecks: A=a⋅b

Umfang der Grundfläche: u=a+b+c=11 cm
Die Oberfläche wird in cm2, sprich Quadratzentimeter, angegeben.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
So gehst du bei beliebigen Prismen vor
Prismen können verschiedene Grundflächen haben.
Je nachdem, um welches Prisma es sich handelt, berechnest du mit anderen Formeln
- die Grundfläche G,
- den Umfang der Grundfläche u
- und die Mantelfläche M.
| Grundfläche des Prismas | Formeln |
|---|---|
| Dreieck | G=12⋅g⋅h |
| u=a+b+c | |
| M=(a+b+c)⋅hk | |
| Parallelogramm | G=a⋅h |
| u=2⋅a+2⋅b | |
| M=(2⋅a+2⋅b)⋅hk | |
| Trapez | G=a+c2⋅h |
| u=a+b+c+d | |
| M=(a+b+c+d)⋅hk |
Dann berechnest du immer:
Oberfläche = 2 ⋅ Grundfläche + Mantelfläche
O=2⋅G+M
M=u⋅hk
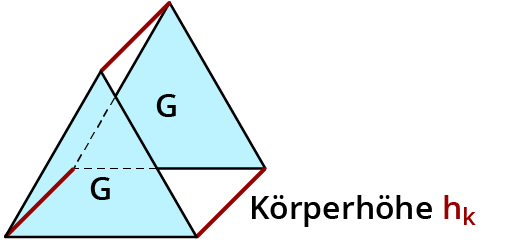
Die Körperhöhe hk ist die Strecke, die die beiden Grundflächen miteinander verbindet.

Kennst du noch Würfel und Quader?
Würfel und Quader sind besondere Prismen. Sie haben einfachere Formeln, mit denen du die Oberfläche berechnest.
Diese Formeln hast du schon gelernt:
| Grundfläche des Prismas | Formeln | |
|---|---|---|
| Quadrat | O=6⋅a2 | |
| Rechteck | O=2⋅ab+2⋅ac+2⋅bc | |
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen