Was ist ein Prisma?

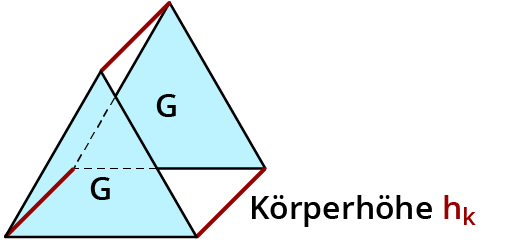
Ein Prisma ist ein Körper. Er hat zwei Grundflächen und eine Mantelfläche.

Die Grundflächen können beliebige Vielecke sein. Sie sind parallel und deckungsgleich.

Die Mantelfläche besteht aus Rechtecken. Der Abstand zwischen den Grundflächen ist die Körperhöhe $$h_k$$.

Verschiedene Prismen

Es gibt viele verschiedene Prismen, je nachdem, welche Grundfläche sie haben.

Auch Würfel und Quader sind Prismen.

Grundfläche des Prismas	Prisma
Quadrat	Würfel Jede Fläche kann die Grundfläche sein, da sie alle parallel und deckungsgleich sind.
Rechteck	Quader Jede Fläche kann die Grundfläche sein, da je zwei parallel und deckungsgleich sind.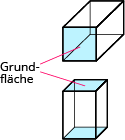
Dreieck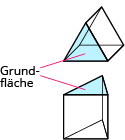
Parallelogramm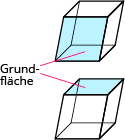
Trapez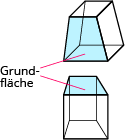

Das Netz eines Prismas

Wenn du das Prisma zu einem Netz ausklappt, kannst du alle äußeren Flächen gut erkennen:

Du siehst die Mantelfläche und zweimal die Grundfläche. Man nennt diese äußeren Flächen des Prismas seine Oberfläche.

Wenn du das Netz eines Prismas zeichnest, ist es am übersichtlichsten, wenn du alle Flächen der Mantelfläche nebeneinander, die Grundflächen oben und unten zeichnest. Alle Flächen behalten dabei ihre Originalgröße.

Das Schrägbild eines Prismas

So zeichnest du ein Schrägbild:

1. Grundfläche in Originalgröße zeichnen

2. Senkrecht nach hinten laufende Kanten (Körperhöhe $$h_k$$) in halber Länge unter 45° zeichnen

3. Fehlende Kanten ergänzen, unsichtbare Kanten gestrichelt.

Das Schrägbild eines Prismas

So zeichnest du ein Schrägbild, bei dem das Prisma auf seiner Grundfläche stehen soll:

1. Grundfläche in Originalgröße zeichnen

2. Höhe $$h_c$$ zeichnen und messen, Teilstrecke $$x$$ messen.

3. Schrägbild der Grundfläche zeichnen: $$c$$ zeichnen, $$x$$ abtragen, $$h_c$$ in halber Länge unter 45° zeichnen.

4. In den Eckpunkten die Körperhöhen $$h_k$$ zeichnen und die Endpunkte zur Deckfläche verbinden.