Zusammengesetzte Körper: Volumen

Viele Gegenstände sind aus geometrischen Körpern zusammengesetzt.

Beispiel: Diese Verpackung besteht aus einem Quader und einem Dreiecksprisma.

Teile zusammengesetzte Körper in einzelne Körper auf, von denen du das Volumen schon berechnen kannst. Anschließend rechnest du die Volumina zusammen.

Jetzt wird gerechnet

Die Verpackung hat folgende Maße.

Weg 1

1. Quader:

$$V_1 = a * b *c$$

$$V_1 = 5cm * 3cm * 4cm$$

$$V_1 = 60cm^3$$

2. Dreiecksprisma:

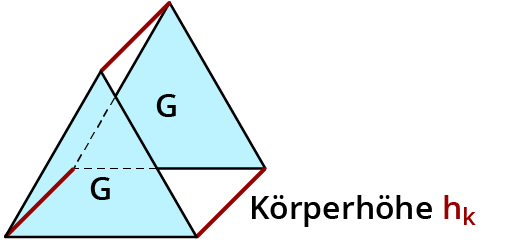
$$V_2 = G * h_k$$

$$V_2 = 1/2 g * h * h_k$$

$$V_2 = 1/2 * 5cm * 5cm * 3cm$$

$$V2 = 37,5cm^3$$

3. Gesamter Körper:

$$V = V_1 + V_2$$

$$V = 60cm^3 + 37,5cm^3$$

$$V = 97,5cm^3$$

So geht’s auch

Weg 2

Du kannst die Verpackung auch als großes Prisma sehen. Die Vorderseite wird zur Grundfläche. Dann brauchst du bloß Grundfläche $$*\ h_k$$ rechnen.

Grundfläche $$=$$ Rechteck $$+$$ Dreieck

$$G = a*b + 1/2 * g *h$$

$$G = 5 cm * 4 cm + 1/2 *5 cm * 5 cm$$

$$G = 32,5 cm^2$$

$$V = G * h_k$$

$$V = 32,5 cm² * 3 cm$$

$$V = 97,5 cm^3$$

Volumen zusammengesetzter Körper

Meist gibt es mehrere Möglichkeiten, wie du das Volumen zusammengesetzter Körper berechnen kannst.

Beispiel

Gegeben ist ein zusammengesetzter Körper aus Quadern mit folgenden Seitenlängen in $$cm$$:

1. Volumina addieren

a)

Quader 1:

$$V_1 = a * b *c$$

$$V_1 = 50\ cm * 30\ cm * 20\ cm$$

$$V_1 = 30000\ cm^3$$

Quader 2:

$$V_2 = 30\ cm * 60\ cm * 20\ cm$$

$$V_2 = 36000\ cm^3$$

Gesamter Körper:

$$V = V_1 + V_2$$

$$V = 30000\ cm^3 + 36000\ cm^3$$

$$V = 66000\ cm^3$$

b)

Quader 1:

$$V_1 = 80\ cm * 30\ cm * 20\ cm$$

$$V_1 = 48000\ cm^3$$

Quader 2:

$$V_2 = 30\ cm * 30\ cm * 20\ cm$$

$$V_2 = 18000\ cm^3$$w

Gesamter Körper:

$$V = V_1 + V_2$$

$$V = 48000\ cm^3 + 18000\ cm^3$$

$$V = 66000\ cm^3$$

Volumen zusammengesetzter Körper

2. Großer Quader und Lücke abziehen

Quader 1:

$$V_1 = 80\ cm * 60\ cm * 20\ cm$$

$$V_1 = 96000\ cm^3$$

Quader 2:

$$V_2 = 50\ cm * 30\ cm * 20\ cm$$

$$V_2 = 30000\ cm^3$$

Gesamter Körper:

$$V = V_1 - V_2$$

$$V = 48000\ cm^3 - 18000cm^3$$

$$V = 66000\ cm^3$$

Noch ein Beispiel

Dieser Körper enthält einen Zylinder.

1. Zylinder:

$$V_1 = G * h_k$$

$$V_1 = π * r^2 * h_K$$

$$V_1= π * (2\ cm)^2 * 8\ cm$$

$$V_1= π * 4\ cm^2 * 8\ cm$$

$$V_1= 12,57\ cm^2 * 8\ cm$$

$$V_1 = 100,53\ cm^3$$

2. Quader:

$$V_2 = a * b *c$$

$$V_2 = 6\ cm * 6cm * 2cm$$

$$V_2 = 72\ cm^3$$

1. Gesamter Körper:

$$V = V_1 + V_2$$

$$V = 100,53\ cm^3 + 72\ cm^3$$

$$V = 172,53\ cm^3$$

Jetzt kommt die Oberfläche

Die Oberfläche zu berechnen ist etwas schwieriger.

Der Oberflächeninhalt eines zusammengesetzten Körpers sind alle Flächen, die du berühren kannst. Deshalb kannst du nicht einfach die Oberflächeninhalte der einzelnen Körper zusammenrechnen. Manche Flächen liegen aneinander. Die darfst du dann nicht mit in den Oberflächeninhalt einrechnen.

Berechne den Oberflächeninhalt.

Wenn du die Packung hinlegst, siehst du besser, dass es ein Prisma ist. Berechne 2 mal die Grundlfäche und die Mantelfläche am Stück. Für die Mantelfläche brauchst du den Umfang.

Oberfläche zusammengesetzter Körper

Nun kannst du wie gewohnt vorgehen:

1. Grundfläche berechnen (Rechteck + Dreieck):

$$G = a * b + 1/2 g * h$$

$$G = 5\ cm * 4\ cm + 1/2 5\ cm * 5\ cm$$

$$G = 20\ cm^2 + 12,5\ cm^2$$

$$G = 32,5\ cm^2$$

2. Mantelfläche berechnen:

$$M = u * h_k$$

$$M = (5\ cm +4\ cm + 5,59\ cm + 5,59\ cm + 4\ cm) * 3\ cm$$

$$M = 24,18\ cm * 3\ cm$$

$$M = 72,54\ cm^2$$

3. Oberfläche berechnen:

$$O = 2 * G + M$$

$$O = 2 * 32,5\ cm^2 + 72,54\ cm^2$$

$$O = 137,54\ cm^2$$