Den Flächeninhalt von Kreisen untersuchen
Flächeninhalt eines Kreises
Die Formel zur Berechnung des Flächeninhalts $$A$$ eines Kreises mit dem Radius $$r$$ lautet:
$$A=pi r^2$$.
Wenn dich interessiert, wie man die Formel begründen kann, dann schau dir die nächste Seite an.
$$pi$$ ist keine rationale Zahl. Das heißt, sie ist nicht als Bruch darstellbar und hat unendlich viele Stellen nach dem Komma.
$$pi$$ $$approx$$ 3,14
Flächeninhalt eines Kreises
Nimm einen beliebig großen Kreis und unterteile diesen in beliebig viele gleich große Teile (beispielsweise 16 Teile).
Zerschneide nun die Kreisfläche in diese 16 Teile und lege 15 davon so nebeneinander, dass sie eine Figur ergeben, die einem Rechteck ähnelt. (Der 16. Teil wird halbiert und links und rechts angelegt.)
Der Flächeninhalt des so entstandenen Rechtecks wird berechnet durch Länge mal Breite.
Die Länge dieses gebastelten Rechtecks entspricht in etwa dem halben Umfang des Kreises ($$1/2u=1/2*2pir$$).
Die Breite entspricht ungefähr dem Radius $$r$$.
Demnach gilt:
$$A$$ $$=$$ Länge mal Breite
$$A = 1/2*2pir*r$$
$$A = pir^2$$
Flächeninhalt eines Kreises:
$$A = pir^2$$
Hinweis: Wenn du keinen Taschenrecher mit $$pi$$-Taste hast, rechne mit $$pi approx 3,14$$.
Flächeninhalt eines Kreises:
$$A = pir^2$$
Hinweis: Wenn du keinen Taschenrecher mit $$pi$$-Taste hast, rechne mit $$pi approx 3,14$$.
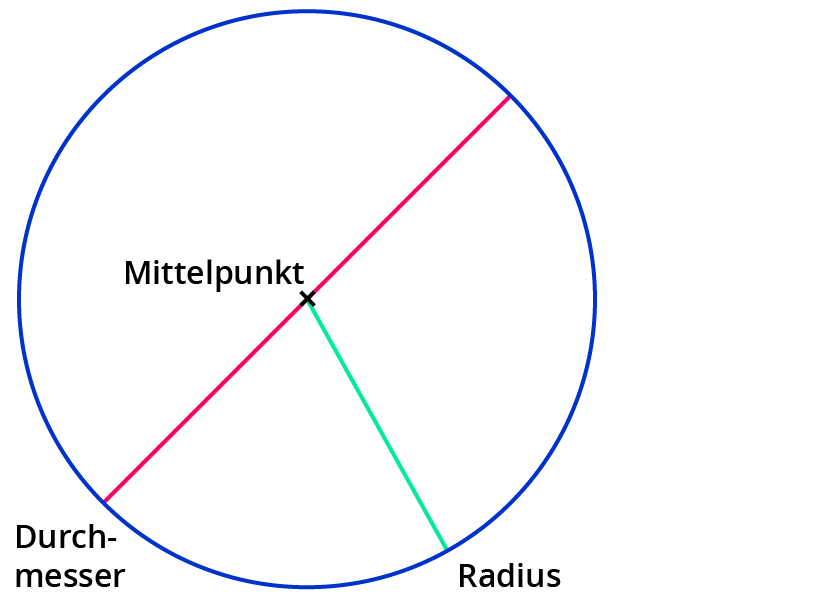
Linien im Kreis
Zur Erinnerung:
Der Durchmesser ist das Doppelte vom Radius.
$$d = 2*r$$
Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Berechnung des Flächeninhalts bei gegebenem Radius
Berechne den Flächeninhalt der Uhr, die du im Bild siehst. Der Radius der Uhr beträgt $$15$$ $$cm$$.
$$A = pi * r^2$$
$$A = pi * (15 cm)^2$$
$$A = pi * 225 cm^2$$
$$A approx 706,9 cm^2$$
Die Fläche der Uhr beträgt also ungefähr $$706,9 cm^2$$.
$$A = pir^2$$
Berechnung des Flächeninhalts bei gegebenem Durchmesser
Im Restaurant bekommst du dein Getränk oft mit einem Pappuntersetzer. Die runden Untersetzer haben einen Durchmesser von $$d = 107$$ $$mm$$. Berechne den Flächeninhalt.
Um die Flächenformel anwenden zu können, benötigst du zunächst den Radius.
$$r = d/2 = (107 mm)/2 = 53,5 mm$$
Nun kannst du die Fläche berechnen.
$$A = pi r^2$$
$$A = pi * (53,5 mm)^2$$
$$A approx 8992 mm^2$$
Die Fläche des Bierdeckels beträgt also ungefähr $$8992$$ $$mm^2$$ oder umgerechnet $$89,92$$ $$cm^2$$.
$$A = pir^2$$
$$r=d/2$$
Bild: fotolia.com (contrastwerkstatt)
Berechnung des Radius und des Durchmessers bei gegebenem Flächeninhalt
Der Flächeninhalt einer Frisbeescheibe ist gegeben mit $$530$$ $$cm^2$$. Berechne den Radius und den Durchmesser der Frisbeescheibe.
$$A = pir^2$$
$$530 cm^2 = pir^2$$
$$(530 cm^2)/pi = r^2$$
$$sqrt((530 cm^2)/pi) = r$$
$$13 cm approx r$$
Der Radius der Frisbeescheibe beträgt ungefähr $$13$$ $$cm$$.
Da du weißt, dass der Durchmesser das Doppelte vom Radius ist, musst du das Ergebnis nur mal zwei nehmen, um den Durchmesser zu berechnen.
Der Durchmesser der Frisbeescheibe beträgt demach ungefähr $$26$$ $$cm$$.
$$A = pi * r^2$$
$$r = sqrt(A/pi)$$
$$d = 2r$$
Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Flächeninhalt eines Kreisrings
Der Durchmesser der abgebildeten CD beträgt $$12$$ $$cm$$ und der Radius demnach $$6$$ $$cm$$.
Bild: Anders ARTig Werbung + Verlag GmbH
Berechne den Flächeninhalt.
$$A = pir^2$$
$$A = pi (6 cm)^2$$
$$A approx 113 cm^2$$
Nun hat die CD aber ein Loch. Demnach müssen wir den Flächeninhalt des Lochs von unserem Ergebnis abziehen.
Der Durchmesser des Lochs beträgt $$1,5$$ $$cm$$. Demnach beträgt der Radius des Lochs $$0,75$$ $$cm$$ und der Flächeninhalt ungefähr $$1,77$$ $$cm^2$$.
$$A = pir^2$$
$$A = pi (0,75 cm)^2$$
$$A approx 1,77 cm^2$$
Der eigentliche Flächeninhalt der CD beträgt also $$111,23$$ $$cm^2$$.
$$113$$ $$cm^2$$ $$-$$ $$1,77$$ $$cm^2$$ $$=$$ $$111,23$$ $$cm^2$$.
$$A = pi * r^2$$
$$r = d/2$$
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen
