Den Umfang von Kreisen berechnen
Was ist Pi ($$pi$$)?
Suche dir einige runde Gegenstände. Miss jeweils den Durchmesser und den Umfang des Gegenstandes.
Den Umfang kannst du messen, indem du einen Faden um den Gegenstand legst und dann die Länge des Fadens misst.
Berechne dann noch jeweils das Verhältnis von Umfang und Durchmesser, also $$u/d$$.
Bereits in der Bibel gibt es Hinweise darauf, dass die Menschen das Verhältnis von Umfang und Radius untersucht haben.
Dem griechischen Mathematiker Archimedes gelang es um 250 v. Chr. erstmals, diese Verhältnis mathematisch einzugrenzen.
Heute wissen wir, dass das Verhältnis von Umfang zu Durchmesser immer gleich $$pi$$ ist.
Was ist Pi ($$pi$$)?
Hier sind Christians und Tamaras Ergebnisse.
| Umfang $$u$$ | Durchmesser $$d$$ | $$u/d$$ | |
|---|---|---|---|
| Becher | 27 cm | 8,5 cm | 3,18 |
| Armreif | 18 cm | 5,8 cm | 3,10 |
| Federtasche | 21 cm | 6,5 cm | 3,23 |
| Ball | 100 cm | 32 cm | 3,13 |
Das Verhältnis von Umfang zu Durchmesser immer gleich $$pi$$.
$$pi$$ ist eine irrationale Zahl mit unendlich viel Nachkommastellen.
$$pi$$ = 3,141592654 ….
Christian und Tamara sind mit ihren Berechnungen also schon sehr nah am richtigen Ergebnis. Die Abweichungen ergeben sich durch Messungenauigkeiten.
$$pi$$ ist keine rationale Zahl. Das heißt, sie ist nicht als Bruch darstellbar und hat unendlich viele Stellen nach dem Komma.
$$pi$$ $$approx$$ 3,14
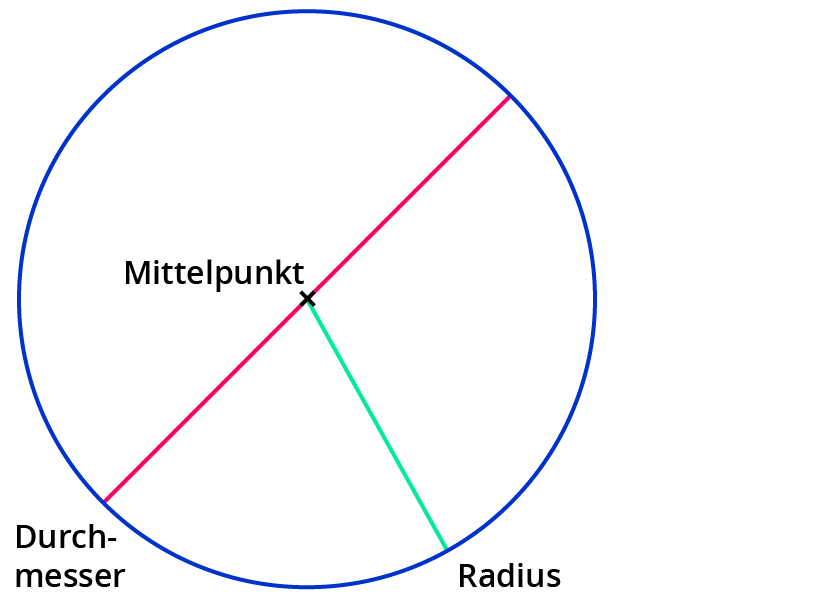
Linien im Kreis
Zur Erinnerung:
Der Durchmesser ist das Doppelte vom Radius.
$$d = 2*r$$
Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Die Umfangsformel
Wenn du bei einem beliebigen Kreis den Umfang (u) durch den Durchmesser (d) teilst, erhältst du immer die Zahl $$pi$$.
Es gilt also:
$$pi = u/d$$
Daraus erhälst du die Umfangsformel für den Kreis.
$$u = pi * d$$
oder wegen $$d = 2*r$$
$$u = 2 * pi * r$$
Hinweis: Wenn du keinen Taschenrecher mit $$pi$$-Taste hast, rechne mit $$pi approx 3,14$$.
$$pi = $$ Umfang (u) geteilt durch Durchmesser (d)
$$pi = u/d rArr u = pi*d$$
oder
$$u = 2 * pi * r$$
Berechnung des Umfangs bei gegebenem Durchmesser
Wie weit rollt ein Rad mit dem Durchmesser $$d = 70$$ cm mit genau einer Umdrehung?
Mit genau einer Umdrehung legt ein Rad genau die Strecke des Umfangs zurück. Wende einfach nur die Formel an.
$$u = pi * d$$
$$u = pi * 70$$ cm
$$u approx 219,9$$ cm $$approx$$ $$2,2$$ m
Mit einer vollen Umdrehung legt das Rad also ungefähr $$2,2$$ m zurück.
$$u = pi * d$$
$$u = 2 * pi * r$$
Berechnung des Umfangs bei gegebenem Radius
Die Erde hat einen Radius von etwa $$6370$$ km.
Berechne die Länge des Äquators, also den Umfang der Erde.
(Die Erde ist zwar nicht ganz genau eine Kugel. Aber das kannst du vernachlässigen.)
$$u = 2 * pi * r$$
$$u = 2 * pi * 6370$$ km
$$u approx 40.024$$ km
Die Länge des Äquators beträgt ungefähr $$40.024$$ km.
$$u = pi * d$$
$$u = 2 * pi * r$$
Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Berechnung des Durchmessers und des Radius bei gegebenem Umfang
Du misst den Umfang eines Glases mit $$21$$ cm.
Berechne den Durchmesser und auch den Radius des Glases.
$$d = u/pi$$
$$d = (21 cm)/pi$$
$$d approx 6,68$$ cm
Der Durchmesser des Glases beträgt ungefähr $$6,68$$ cm.
Da du weißt, dass der Durchmesser das Doppelte vom Radius ist, musst du das Ergebnis nur durch zwei teilen, um den Radius zu berechnen.
Der Radius des Glases beträgt demach ungefähr $$3,34$$ cm.
$$u = pi * d$$
$$u = 2 * pi * r$$
$$d = u/pi$$
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen
