Geraden am Kreis

Es gibt drei verschiedene Möglichkeiten der Lagebeziehungen für eine Gerade und einen Kreis.

1. Sekante:
   Kreis und Gerade schneiden sich in genau zwei Punkten.

2. Tangente:
   Kreis und Gerade berühren sich in genau einem Punkt.

3. Passante:
   Kreis und Gerade schneiden oder berühren sich nicht.

Eigenschaften

Die Sekante, die Tangente und die Passante sind alle drei Geraden. Das bedeutet, alle drei sind unendlich lange, gerade Linien ohne Anfang und ohne Ende.

Die Tangente hat zusätzlich noch die Eigenschaft, dass sie im Berührpunkt senkrecht (orthogonal) zum entsprechenden Radius steht.

Weitere Linien am Kreis

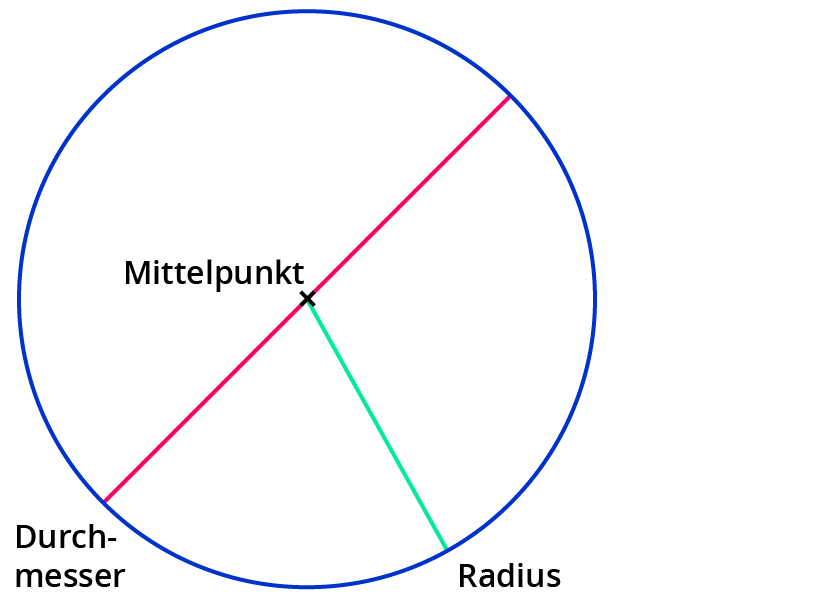
Neben dem Radius und dem Durchmesser gibt es auch noch die Sehne im Kreis. Alle drei Linien sind keine Geraden, sondern Strecken, da sie einen Anfang und ein Ende haben.

Eine Sehne ist eine Verbindungsstrecke von zwei Punkten auf der Kreislinie. So ist der Durchmesser ein Spezialfall der Sehne. Er ist eine Verbindungsstrecke, die durch den Mittelpunkt des Kreises verläuft.

Konstruktion der Geraden

Eine Passante (kein Berührungspunkt) und eine Sekante (zwei Schnittpunkte) haben keine weiteren Eigenschaften, so dass deren Konstruktion keine besonderen Schritte erfordert.

Die Tangente steht im Berührpunkt jedoch senkrecht (orthogonal) zum entsprechenden Radius. Diese Eigenschaft must du bei der Konstruktion einer Tangenten berücksichtigen.

Konstruktion einer Tangenten mit P auf dem Kreis

Konstruiere die Tangente an dem Kreis durch den Punkt P.

1. Zeichne durch den Mittelpunkt M und den Punkt P einen Strahl (von M aus).
   
   
   
   
2. Zeichne eine Senkrechte zu diesem Strahl durch den Punkt P. Das kannst du mit deinem Geodreieck machen. Die so erhaltene Senkrechte ist die gesuchte Tangente.

Konstruktion einer Tangenten mit P außerhalb des Kreises

Konstruiere die Tangente an dem Kreis durch den Punkt P, wenn P außerhalb des Kreises liegt.

1. Verbinde den Mittelpunkt $$M$$ des gegebenen Kreises und den außerhalb liegende Punkt $$P$$.
   
   
   
   
2. Konstruiere den Mittelpunkt der Strecke $$bar(MP)$$. Bezeichne den Mittelpunkt mit $$Q$$. (Kreisbögen um M und P mit beliebiger Zirkelspanne, aber größer als der Radius; Schnittpunkte der Kreise verbinden, Schnittpunkt mit $$bar(MP)$$ ist $$Q$$.)
   
   
   
   
3. Zeichne um $$Q$$ einen Kreis mit dem Durchmesser $$bar(MP)$$.
   
   
   
   
4. Es entstehen die Schnittpunkte $$T_1$$ und $$T_2$$.
   
   
   
   Die Winkel an den Punkten $$T_1$$ und $$T_2$$ sind nach dem Satz des Thales rechte Winkel.
   
   
   
   
5. Zeichne eine Gerade durch $$T_1$$ und $$P$$ und eine Gerade durch $$T_2$$ und $$P$$. Das sind die gesuchten Tangenten.