Die Umfangsformel und die Flächenformel

Erinnerst du dich, wie du den Umfang und wie du die Fläche eines Kreises berechnest?

Umfang: `u = pi * d` oder `u = 2 * pi * r`

Fläche: `A = pi * r^2`

Hinweis: Wenn du keinen Taschenrecher mit `pi`-Taste hast, rechne mit `pi approx 3,14`.

Kreisbogen

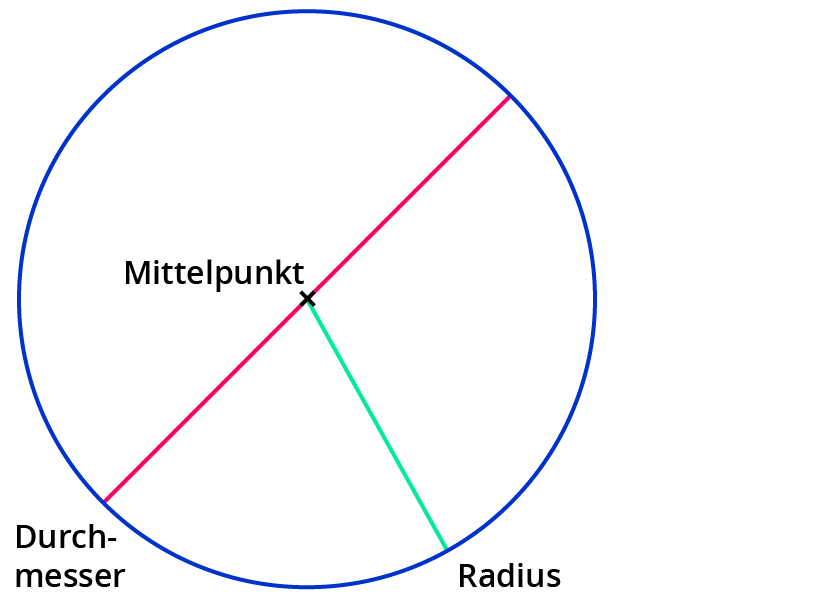
Ein Teil eines Kreises heißt Kreissektor oder Kreisausschnitt.
Der Teil des Umfangs, der zu diesem Kreissektor gehört, heißt Kreisbogen. Er wird mit `b` bezeichnet.

Der Anteil des Kreisbogens am gesamten Umfang entspricht dem Anteil des Winkels an 360° (gesamter Kreis).

Hier siehst du Anteile, die häufig vorkommen:

`90°``:` `(90°)/(360°) = 1/4` `rarr` Viertelkreis

`180°``:` `(180°)/(360°) = 1/2` `rarr` Halbkreis

`270°``:` `(270°)/(360°) = 3/4` `rarr` Dreiviertelkreis

Anteil des Umfangs mal gesamter Umfang ergibt den Kreisbogen `b`.

`b = alpha/(360°) * pi * d` oder

`b = alpha/(360°) * 2 * pi * r`

Rechnen mit der Kreisbogenformel

Sei der Kreissektor durch `alpha = 40°` gegeben. Der Durchmesser des Kreises ist `d = 8` `cm`.

Berechne den Kreisbogen `b`.

`b = alpha/(360°) * pi * d`

`b = (40°)/(360°) * pi * 8` cm

`b = 1/9 * pi * 8` cm

`b approx 2,79` cm

Die Länge des Kreisbogens beträgt ungefähr `2,79` cm.

Noch ein Beispiel

Sei der Kreissektor durch `alpha = 40°` gegeben. Die Länge des Kreisbogens beträgt `b = 5` `cm`.

Berechne den Durchmesser `d` des Kreises.

`b = alpha/(360°) * pi * d`

`5   cm = (40°)/(360°) * pi * d`

`5   cm = 1/9 * pi * d`

Löse die Gleichung nach `d` auf.

Es gilt:

`d = (9*5   cm)/pi`

`d approx 14,32` cm.

Der Durchmesser des Kreises beträgt ungefähr `14,32` `cm`.

Kreissektor

Ein Kreissektor wird mit `A_s` bezeichnet.

Der Anteil des Kreissektors am gesamten Umkreis entspricht dem Anteil des Winkels an 360° (gesamter Kreis).

Diese Anteile kommen häufig vor:

`90°``:` `(90°)/(360°) = 1/4` `rarr` Viertelkreis

`180°``:` `(180°)/(360°) = 1/2` `rarr` Halbkreis

`270°``:` `(270°)/(360°) = 3/4` `rarr` Dreiviertelkreis

Anteil der Kreisfläche mal ganzer Kreis ergibt den Kreissektor `A_s`.

`A_s = alpha/(360°) * pi * r^2`

Rechnen mit der Kreissektorformel

Sei der Kreissektor durch `alpha = 40°` gegeben. Der Kreis hat einen Durchmesser von `d = 8` cm (`rArr` `r=4` cm).

Berechne den Kreissektor `A_s`.

`A_s = alpha/(360°) * pi * r^2`

`A_s = (40°)/(360°) * pi * (4 cm)^2`

`A_s = 1/9 * pi * 16` `cm^2`

`A_s approx 5,6` `cm^2`

Der Flächeninhalt des Kreissektors beträgt ungefähr `5,6` `cm^2`.

Rechnen mit der Kreissektorformel

Sei der Kreissektor durch `alpha = 40°` gegeben. Der Flächeninhalt des Kreissektor beträgt `A_s=10` `cm^2`.

Berechne den Durchmesser `d` des Kreises.

`A_s = alpha/(360°) * pi * r^2`

`10 cm^2 = (40°)/(360°) * pi * r^2`

`10 cm^2 = 1/9 * pi * r^2`

Löse die Gleichung nach `r` auf.

Es gilt:

`r^2 = (9*10 cm)/(pi)`

`r = sqrt( (9*10  cm)/(pi)`

`r approx 5,35` `cm`

Der Radius des Kreises beträgt also ungefähr `r=5,35` `cm`. Also beträgt der Durchmesser des Kreises ungefähr `d=10,7` `cm`.