Koordinaten eines Vektors

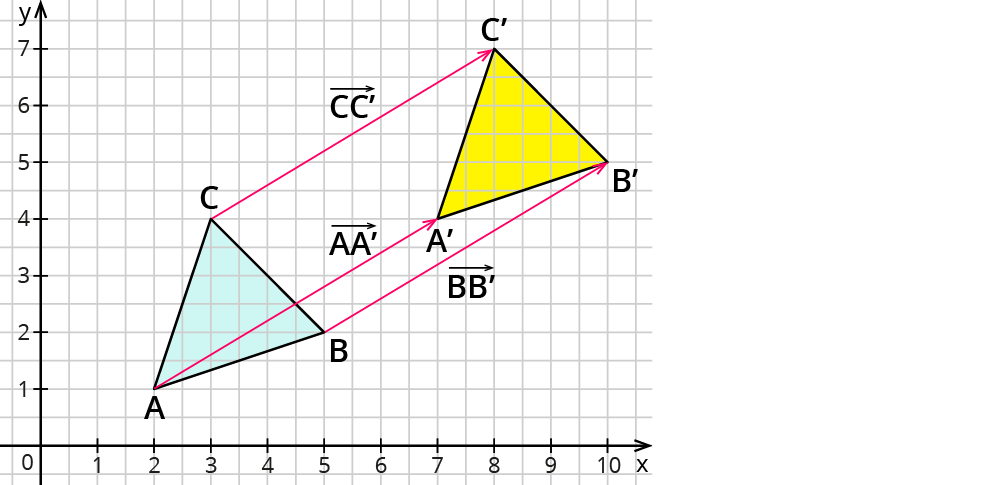
Ein Vektor kann dir anzeigen, wie weit ein Punkt verschoben wird. Du kannst entweder zählen, wie viele Einheiten nach rechts bzw. links und oben bzw. unten verschoben wird, oder du nimmst den Start- und Endpunkt des Vektors zu Hilfe.

Dann erhältst Du die Koordinaten des Pfeils $$vec {\A\A’}$$ - oder gleichbedeutend des Vektors $$vec v$$ - aus der Differenz der Koordinaten des Startpunktes $$A(x|y)$$ und denen des Endpunktes $$A’(x’|y’)$$. Du rechnest wie in der Abbildung angegeben:

$$vec v = ((v_x),(v_y))= ((x’ - x),(y’ - y))$$.

Der Vektor $$vec {\A\A’}$$ aus der Abbildung ist also:

$$vec {\A\A’} = vec v = ((7 - 2),(4 - 1)) = ((5),(3))$$.

Der Vektor $$vec {\A\A’}$$ aus der Abbildung ist also:

$$vec {\A\A’} = vec v = ((7 - 2),(4 - 1)) = ((5),(3))$$.

Ortspfeile und Ortsvektoren

Wie in der Abbildung zu sehen ist, können beliebig viele Pfeile den Vektor $$vec v = ((5),(3))$$ darstellen. Sie alle haben dieselbe Richtung und Länge, nur andere Start- bzw. Endpunkte.

Einer der Pfeile - er ist rot markiert - fällt auf. Er hat als Startpunkt den Nullpunkt des Koordinatensystems $$O(0|0)$$ und als Endpunkt genau die Koordinaten $$(5|3)$$ des Vektors $$((5),(3))$$.
Ein Pfeil dieser Art mit dem Startpunkt $$O(0|0)$$ wird als Ortspfeil und der entsprechende Vektor als Ortsvektor bezeichnet.

Gegenvektor

Im Bild siehst du einen Vektor $$vec v = vec {\A\A’} = ((4),(3))$$, der den Punkt $$A$$ zum Punkt $$A’$$ verschiebt. Ein zweiter Vektor $$vec v’ = vec {\A’\A} = ((-4),(-3))$$ macht diese Verschiebung wieder rückgängig. Ein Vektor mit dieser Eigenschaft wird als Gegenvektor bezeichnet.

Vektor, Gegenvektor und Punktkoordinaten

Der Vektor $$vec v = ((5),(3))$$ verschiebt den Punkt $$A(-2|2)$$ zum Punkt $$A’(3|5)$$.
Der Gegenvektor $$vec v’ = ((-5),(-3))$$ verschiebt den Punkt $$A’$$ zum Punkt $$A$$.

Auch wenn Du nur einen Punkt mit einem Vektor vorliegen hast, kannst du nun den zugehörigen End- oder Startpunkt berechnen.

Berechnung des Endpunktes

Addiere die Koordinaten des Vektors $$vec v$$ zu den Punktkoordinaten des Startpunktes $$A$$:
$$(-2 + 5| 2 + 3) rarr (3|5)$$.
Der Endpunkt hat also die Koordinaten $$A’(3|5)$$.

Berechnung des Startpunktes

Addiere die Koordinaten des Gegenvektors $$vec v’$$ zu den Punktkoordinaten des Endpunktes $$A’$$:
$$(3 + (-5)| 5 + (-3)) rarr (-2|2)$$.
Der Startpunkt hat also die Koordinaten $$A(-2|2)$$.

Berechnung der Punktkoordinaten des Startpunktes $$A$$

Addiere die Koordinaten des Gegenvektors $$vec v’$$ zu den Punktkoordinaten des Endpunktes $$A’$$: $$(3 + (-5)| 5 + (-3)) rarr (-2|2)$$.
Der Startpunkt hat die Koordinaten $$A(-2|2)$$.