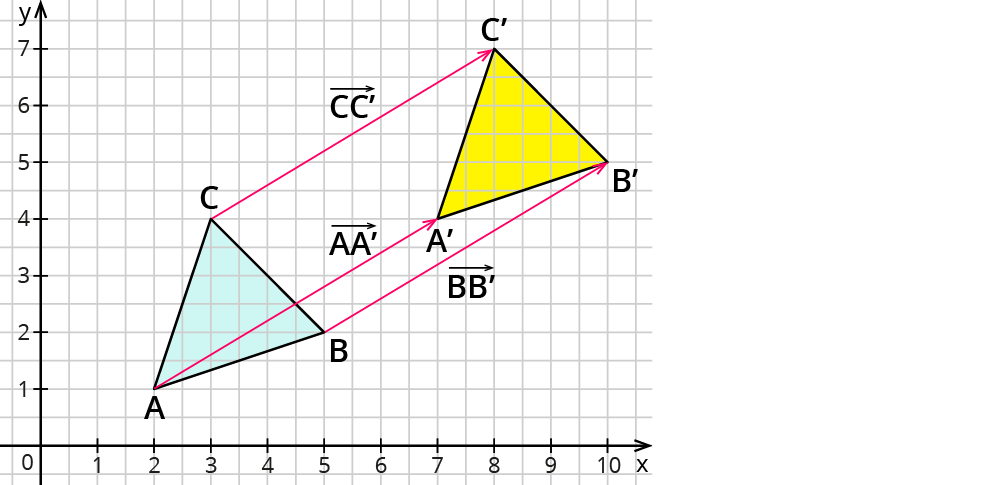
Vektorenaddition
Addition von Vektoren
Wenn ein Vektor durch einen Pfeil vom Punkt $$A$$ zum Punkt $$B$$ repräsentiert wird, schreibst du $$vec v = vec (\A\B)$$. In der Abbildung entspricht der Vektor $$vec (\A\B)$$ der Bewegung eines Objektes von $$A$$ nach $$B$$ Bewegt sich das Objekt anschließend von $$B$$ nach $$C$$, so kannst du diese Bewegung durch den Vektor $$vec (BC)$$ darstellen.
Natürlich kann sich das Objekt aber auch gleich von $$A$$ nach $$C$$ bewegen! Das Ergebnis der beiden Bewegungen ist dasselbe. Du kannst also schreiben:
$$vec (\A\B) + vec (BC) = vec (\A\C)$$.
Somit hast Du zwei Vektoren miteinander addiert und wieder einen Vektor erhalten!
Bei dieser Vektoraddition heißt $$vec (\AC)$$ auch die Vektorsumme von $$vec (\A\B)$$ und $$vec (BC)$$.
Verschiedene Wege führen zum Ziel
Die Addition von zwei Vektoren ist eine kommutative Rechenoperation, das heißt, dass die Vektoren in beliebiger Reihenfolge addiert werden können.
Du kannst in der Abbildung erkennen, dass die Reihenfolge der Addition der Vektoren keinen Einfluss auf das Ergebnis hat. In beiden Fällen erhältst du
$$vec v_1 + vec v_2 =vec v_2 + vec v_1 = vec v$$.
Zeichnest du beide Möglichkeiten, zwei Vektoren zu addieren, in ein einziges Diagramm, erhältst zu ein sogenanntes Vektorparallelogramm. Dieses wird gerne zur Lösung bestimmter physikalischer Probleme benutzt.
Addition der Vektorkoordinaten
Um die Koordinaten eines addierten Vektors zu bestimmen, musst du keine Einheiten zählen, sondern kannst die Koordinaten der beiden Summanden zusammenrechnen.
Beispiel
Der Punkt $$A$$ wird in der Abbildung durch den Vektor $$vec v_1 = ((6),(0))$$ zum Punkt $$B$$ verschoben und anschließend durch den Vektor $$vec v_2 = ((2),(3))$$ zum Punkt $$C$$.
Du addierst nun einfach die Koordinaten der Vektoren $$vec v_1$$ und $$vec v_2$$ und erhältst den gesuchten Vektor $$vec v$$:
$$vec v_1 + vec v_2 = ((6),(0))+((2),(3)) = ((6 + 2),(0+3))=((8),(3)) = vec v$$.
Der neue Vektor $$vec v$$ heißt auch Summenvektor.
Die Koordinaten des Summenvektors zweier Vektoren ergeben
sich durch Addition der Einzelvektoren:
$$vec v = vec v_1 + vec v_2 = ((x_1),(y_1))+((x_2),(y_2)) = ((x_1+x_2),(y_1+y_2))$$
Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Mittelpunkt einer Strecke
Die Vektorrechnung kann dir an vielen Stellen behilflich sein, an denen du mit Strecken umgehen musst.
Beispiel: Mittelpunkt einer Strecke
In der Abbildung siehst du eine Strecke von $$A$$ nach $$B$$ mit eingezeichnetem Mittelpunkt $$M$$. Die Koordinaten des Mittelpunktes $$M$$ erhältst du, indem du jeweils die Hälfte der Summe der x-Koordinaten von $$A(2|1)$$ und $$B(8|7)$$ und der y-Koordinaten von $$A$$ und $$B$$ bildest.
Dieses Beispiel kannst du einfach nachrechnen:
$$M(2 + frac(8-2)(2)|1+frac(7-1)(2)) rarr $$
$$M(frac(4+8-2)(2)|frac(2+7-1)(2)) rarr $$
$$M(frac(2+8)(2)|frac(1+7)(2)) rarr $$
$$M(frac(10)(2)|frac(8)(2)) rarr$$
$$M(5|4)$$.
Der Mittelpunkt M(x|y) einer Strecke $$[AB]$$ mit $$A(x_A|y_A)$$ und $$B(x_B|y_B)$$ lässt sich nach folgender Formel berechnen:
$$M(frac(x_A+x_B)(2)|frac(y_A+y_B)(2)) $$.
Schau dir die Abbildung an. Die Koordinaten des Mittelpunktes $$M$$ erhältst du, indem du jeweils die Hälfte der Summe der x-Koordinaten von $$A(2|1)$$ und $$B(8|7)$$ und der y-Koordinaten von $$A$$ und $$B$$ bildest.
Diese Regel wird durch die folgende Rechnung am Beisplel erläutert:
$$M(2 + frac(8-2)(2)|1+frac(7-1)(2)) rarr $$
$$M(frac(4+8-2)(2)|frac(2+7-1)(2)) rarr $$
$$M(frac(2+8)(2)|frac(1+7)(2)) rarr $$
$$M(frac(10)(2)|frac(8)(2)) rarr$$
$$M(5|4)$$.
Der Mittelpunkt M(x|y) einer Strecke $$[AB]$$ mit $$A(x_A|y_A)$$ und $$B(x_B|y_B)$$ lässt sich nach folgender Formel berechnen:
$$M(frac(x_A+x_B)(2)|frac(y_A+y_B)(2)) $$.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen
