Vom Quadrat zur Raute

Bei einem Rechteck und Parallelogramm sind jeweils zwei gegenüberliegende Seiten gleich lang.

Können auch zwei nebeneinander liegende Seiten gleich lang sein?

Ja, nimm ein Quadrat, bei dem ja alle Seiten gleich lang sind. Das Quadrat kannst du drehen, die Seiten kippen und die Figur zusammendrücken. Die benachbarten Seiten bleiben immer gleich lang.

Vom Quadrat zum Drachenviereck

Ziehe an einer Ecke eines Quadrats. Dann kommt so eine Figur heraus:

In der rechten Figur sind 2 benachbarten Seiten gleich lang.

Drachenvierecke können eine einspringende Spitze haben:

Beschriften

Du kannst jeweils denselben Buchstaben verwenden, wenn die Seiten genau gleich lang sind.

Umfang berechnen

Den Umfang des Drachens berechnest du so wie bei anderen Vierecken.

Es gilt die allgemeine Formel:

$$u = a + b + c + d$$

Weil nicht alle Seiten verschieden lang sind, kannst du die Formel vereinfachen:

$$u = a + a + b + b = 2 * a + 2 * b$$

Oder noch einfacher für die Raute:

$$u = a + a + a + a = 4 * a$$

Flächeninhalt berechnen

Bei Parallelogramm oder Trapez war es möglich, mithilfe der Formel $$A = a * b$$ den Flächeninhalt herzuleiten. Beim Drachen laufen die Seiten aber „schief“…

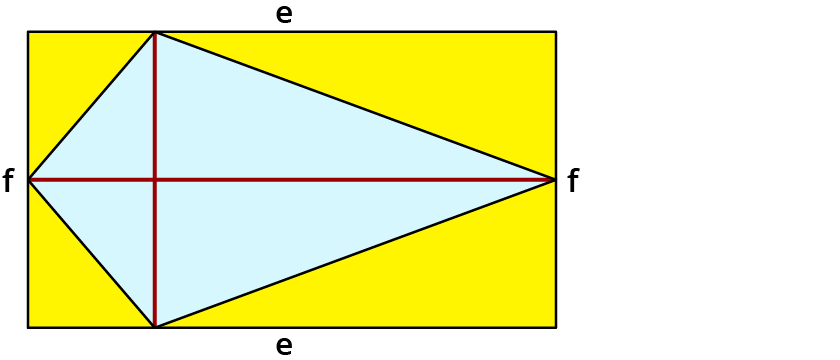
Also müssen irgendwelche Linien her, die senkrecht und waagrecht verlaufen. Den Drachen kannst du so unterteilen:

Die Strecken, die aus dem Drachen vier Dreiecke machen, heißen Diagonalen.

Verdopple jedes Dreieck und lege jeweils 2 gleiche Dreiecke aneinander:

Das entstandene Rechteck hat den doppelten Flächeninhalt wie der Drachen.

Jetzt kommt die Formel

Die ganze Figur ist ja ein Rechteck, also $$A = a * b$$.

Länge und Breite des Rechtecks sind die Diagonalen $$e$$ und $$f$$ des Drachens.

Ersetze das $$a$$ durch $$e$$ und das $$b$$ durch $$f$$:

$$A = e * f$$

Das ist der Flächeninhalt für zwei Drachen.

Wenn du also den erhaltenen Wert halbierst, erhältst du die gewünschte Formel:

$$A = e * f : 2$$

Mathematiker schreiben:

$$A=(e*f)/2$$

Beispiel

Wie groß sind Fläche und Umfang dieses Drachenvierecks?

Um den Flächeninhalt zu berechnen, nimmst du die beiden Diagonalen ($$e$$ und $$f$$) miteinander mal:

$$16 * 9 = 144$$

Das Ergebnis teilst du dann durch $$2$$:

$$144 : 2 = 72$$

Die Fläche des Drachenvierecks ist $$72 cm^2$$ groß.

Die Rechnung in einem Schritt:

$$A = 16 * 9 : 2 = 72$$

Oder genauer (mit den Maßeinheiten):

$$A = 16 cm * 9 cm : 2 = 72 cm^2$$

Umfang

Umfangsformel für Drachenvierecke:

$$u=2*a+2*b$$

$$u = 2 * 13 + 2 * 6 = 38$$

oder genauer (mit den Maßeinheiten):

$$u = 2 * 13 cm + 2 * 6 cm = 38 cm$$

Der Umfang des Drachenvierecks beträgt $$38 cm$$.

Zum Schluss

Was haben Quadrat, Raute und Drachen gemeinsam, was unterscheidet sie?

• Bei allen sind je zwei nebeneinanderliegende Seiten gleich lang.
• Bei Quadrat und Raute sind die diagonal gegenüberliegenden Winkel gleich groß.
• Bei Quadrat und Raute sind alle Seiten gleich lang.
• Bei allen stehen die Diagonalen senkrecht aufeinander.
• Bei Quadrat und Raute werden die Diagonalen im Schnittpunkt halbiert.

Eine Raute ist also auch ein Drachen. Und ein Quadrat ist eine Raute (und damit auch ein Drachen).