Größen umrechnen (Länge, Fläche, Volumen)
Das musst du fürs Umrechnen wissen
Für das Umrechnen von Größen ist es wichtig, dass du
eine Vorstellung von den Einheiten der Größen hast.
die Umrechnungszahlen kennst.
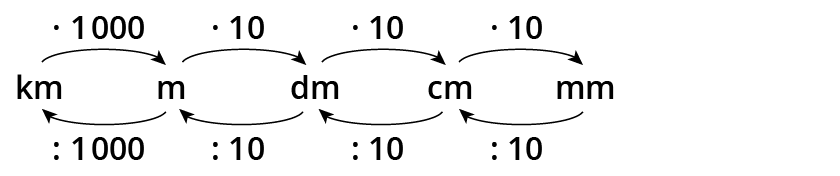
Umrechnungszahlen für Längen
km (Kilometer)
$$:1000$$ ↑ ↓ $$*1000$$
m (Meter)
$$:10$$ ↑ ↓ $$*10$$
dm (Dezimeter)
$$:10$$ ↑ ↓ $$*10$$
cm (Zentimeter)
$$:10$$ ↑ ↓ $$*10$$
mm (Millimeter)
Einheitenkette:
$$1$$ km $$stackrel(*1000)=$$ $$1000$$ m $$stackrel(*10)=$$ $$10000$$ dm $$stackrel(*10)=$$ $$100000$$ cm $$stackrel(*10)=$$ $$1000000$$ mm
$$1$$ m $$stackrel(*10)=$$ $$10$$ dm $$stackrel(*10)=$$ $$100$$ cm $$stackrel(*10)=$$ $$1000$$ mm
$$1$$ dm $$stackrel(*10)=$$ $$10$$ cm $$stackrel(*10)=$$ $$100$$ mm
$$1$$ mm $$stackrel( :10)=$$ $$0,1$$ cm $$stackrel( :10)=$$ $$0,01$$ dm $$stackrel( :10)=$$ $$0,001$$ m $$stackrel( :1000)=$$ $$0,000001$$ km
$$1$$ cm $$stackrel( :10)=$$ $$0,1$$ dm $$stackrel( :10)=$$ $$0,01$$ m $$stackrel( :1000)=$$ $$0,00001$$ km
$$1$$ dm $$stackrel( :10)=$$ $$0,1$$ m $$stackrel( :1000)=$$ $$0,0001$$ km
$$1$$ m $$stackrel( :1000)=$$ $$0,001$$ km
Die Umrechnungszahl für Längen ist $$10$$, nur bei Kilometer zu Meter ist es $$1000$$.
| Einheit | Beispiel |
|---|---|
| $$1$$ mm | Dicke einer 1-Cent-Münze |
| $$1$$ cm | Breite zweier Karos im Heft |
| $$1$$ dm | Handbreite |
| $$1$$ m | Ein großer Schritt |
| $$100$$ m | Laufstrecke im Sportunterricht |
| $$1$$ km | Der Weg, wenn du 15 Minuten langsam gehst |
So rechnest du Einheiten um
Beispiel: Rechne $$5$$ Kilometer in Meter um.
1. Stelle dir die beiden Einheiten vor.
| $$1$$ m | Ein großer Schritt |
| $$1$$ km | Der Weg, wenn du 15 Minuten langsam gehst |
→ Meter ist die kleinere Einheit.
2. Überlege, ob du multiplizieren oder dividieren musst.
| Größere in kleinere Einheit umrechnen. | Der Zahlenwert wird größer. Multipliziere mit der Umrechnungszahl. |
| Kleinere in größere Einheit umrechnen. | Der Zahlenwert wird kleiner. Dividiere durch die Umrechnungszahl. |
→ km in m → die größere in die kleinere Einheit umrechnen → multiplizieren
3. Bestimme die Umrechnungszahl.
$$1000$$
4. Multipliziere oder dividiere mit der Umrechnungszahl.
$$5*1000=5000$$ m
5. Kontrolle: Stelle dir die ungefähre Größe der beiden Angaben vor.
$$1$$ m ist ein großer Schritt. Für $$1$$ km musst du sehr viele Schritte machen. → $$5000$$ m (viele große Schritte) passt.
Umrechnungszahlen für den Flächeninhalt
km2 (Quadratkilometer)
$$:100$$ ↑ ↓ $$*100$$
ha (Hektar)
$$:10000$$ ↑ ↓ $$*10000$$
m2 (Quadratmeter)
$$:100$$ ↑ ↓ $$*100$$
dm2 (Quadratdezimeter)
$$:100$$ ↑ ↓ $$*100$$
cm2 (Quadratzentimeter)
$$:100$$ ↑ ↓ $$*100$$
mm2 (Quadratmillimeter)
Einheitenkette
$$1$$ km2 $$stackrel(*100)=$$ $$100$$ ha $$stackrel(*10000)=$$ $$1000000$$ m2
$$1$$ ha $$stackrel(*10000)=$$ $$10000$$ m2 $$stackrel(*100)=$$ $$1000000$$ dm2
$$1$$ m2 $$stackrel(*100)=$$ $$100$$ dm2 $$stackrel(*100)=$$ $$10000$$ cm2
$$1$$ dm2 $$stackrel(*100)=$$ $$100$$ cm2 $$stackrel(*100)=$$ $$10000$$ mm2
$$1$$ mm2 $$stackrel( :100)=$$ $$0,01$$ cm2 $$stackrel( :100)=$$ $$0,0001$$ dm2
$$1$$ cm2 $$stackrel( :100)=$$ $$0,01$$ dm2 $$stackrel( :100)=$$ $$0,0001$$ m2
$$1$$ dm2 $$stackrel( :100)=$$ $$0,01$$ m2 $$stackrel( :10000)=$$ $$0,000001$$ ha
$$1$$ m2 $$stackrel( :10000)=$$ $$0,0001$$ ha $$stackrel( :100)=$$ $$0,000001$$ km2
Die Umrechnungszahl für den Flächeninhalt ist $$100$$. Nur von Hektar zu Quadratmeter ist es $$10000$$.
| Einheit | Beispiel |
|---|---|
| $$1$$ km2 | Fläche von ca. 200 Fußballfeldern |
| $$1$$ ha | Größe eines Fußballstadions |
| $$100$$ m2 | Hälfte eines Volleyballfeldes |
| $$1$$ m2 | Größe der Seitenfläche einer Schultafel |
| $$1$$ dm2 | 1 Bierdeckel |
| $$1$$ cm2 | 4 Kästchen im Mathematikheft |
| $$1$$ mm2 | Punkt mit einem Filzstift |
Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Umrechnungszahlen für den Rauminhalt (Volumen)
m3 (Kubikmeter)
$$:1000$$ ↑ ↓ $$*1000$$
l (Liter) oder dm3 (Kubikdezimeter)
$$:1000$$ ↑ ↓ $$*1000$$
ml (Milliliter) oder cm3 (Kubikzentimeter)
$$:1000$$ ↑ ↓ $$*1000$$
mm3 (Kubikmillimeter)
Einheitenkette
$$1$$ m3 $$stackrel(*1000)=$$ $$1000$$ l $$stackrel(*1000)=$$ $$1000000$$ ml
$$1$$ l $$stackrel(*1000)=$$ $$1000$$ ml $$stackrel(*1000)=$$ $$1000000$$ mm3
$$1$$ ml $$stackrel(*1000)=$$ $$1000$$ mm3
$$1$$ mm3 $$stackrel( :1000)=$$ $$0,001$$ ml $$stackrel( :1000)=$$ $$0,000001$$ l
$$1$$ ml $$stackrel( :1000)=$$ $$0,001$$ l $$stackrel( :1000)=$$ $$0,000001$$ m3
$$1$$ l $$stackrel( :1000)=$$ $$0,001$$ m3
Die Umrechnungszahl für die Einheiten des Rauminhalts/Volumens ist immer $$1000$$.
| Einheit | Beispiel |
|---|---|
| $$1$$ m3 | Inhalt eines Müllcontainers |
| $$200$$ m3 | Volumen eines Klassenraumes |
| $$1$$ l | Inhalt einer Getränkeflasche |
| $$10$$ l | Inhalt eines Wassereimers |
| $$100$$ l | Inhalt eines großen Aquariums |
| $$1$$ ml / cm3 | Spielwürfel |
| $$200$$ ml | Inhalt einer Tasse |
Die Schrittfolge beim Umrechnen
So rechnest du Einheiten um:
- Stelle dir die beiden Einheiten bildlich vor.
- Überlege, ob du multiplizieren oder dividieren musst:
- Bestimme die Umrechnungszahl.
- Multipliziere bzw. dividiere mit der Umrechnungszahl.
- Kontrolle: Stelle dir die ungefähre Größe der beiden Angaben vor.
| größere in kleinere Einheit umrechnen | Der Zahlenwert wird größer und du multiplizierst mit der Umrechnungszahl. |
| kleinere in größere Einheit umrechnen | Der Zahlenwert wird kleiner und du dividierst durch die Umrechnungszahl. |
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen
