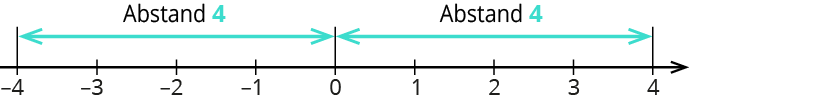Umkehrrechenarten nutzen
Die additive Gegenzahl
Die additive Gegenzahl zu a ist –a. Als Gegenzahl bezeichnest du die Zahl, die in der Addition 0 ergeben.
Beispiel:
Zu 7 ist die Gegenzahl -7.
7+(-7)=0
Zu -5 ist die Gegenzahl 5.
-5+5=0
0 ist das neutrale Element der Addition und Subtraktion. Der Wert des Ergebnisses ändert sich durch +0 nicht.
Beispiel: 8+0=8
In dem Zahlbereich der natürlichen Zahlen gibt es keine Gegenzahlen. Denn alle natürlichen Zahlen sind nicht negativ.
Die multiplikative Gegenzahl
Die multiplikative Gegenzahl zu a ist 1a. Beim Multiplizieren ergeben Zahl und Gegenzahl 1.
Beispiel:
Zu 3 ist die Gegenzahl 13.
3⋅13=1
Betrag einer Zahl
Der Betrag einer Zahl ist der Abstand von der 0. Du schreibst den Betrag einer Zahl in Betragsstriche. |x|

Beispiel:
|4|=4
|-4|=4
Beide Zahlen haben denselben Abstand von der 0.
Bei positiven Zahlen kannst du den Betragsstrich weglassen. Bei negativen Zahlen in Betragsstrichen erhältst du eine positive Zahl.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Nutzen
Mit den Gegenzahlen kannst du Rechnungen vereinfachen.
Beispiel:
7⋅8⋅18+359–7=359
Du siehst gleich, dass 8⋅18=1 ist.
7–7=0
Das Ergebnis der Aufgabe ist 359.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen