Zahlenbereiche untersuchen - mit rationalen Zahlen
Welche Zahlenbereiche gibt es?
Zahlen kannst du je nach Art einem oder mehreren Zahlenbereichen zuordnen. Zahlenbereiche sind Mengen, die Zahlen einer Sorte enthalten.
Diese Zahlenbereiche gibt es:
- Natürliche Zahlen ℕ
- Ganze Zahlen ℤ
- Gebrochene Zahlen ℚ+
- Rationale Zahlen ℚ
- Irrationale Zahlen
Was sind natürliche und ganze Zahlen?
Natürliche Zahlen ℕ
Der Zahlenbereich der natürlichen Zahlen ℕ bildet das Zählen als natürlichen Prozess ab.
Die kleinste natürliche Zahl ist die 0.
Die Menge der natürlichen Zahlen enthält alle Nachfolger der 0 bis unendlich:
ℕ={0,1,2,3,4,…,n,n+1,…} .
Wie kannst du mit natürlichen Zahlen rechnen?
Du darfst uneingeschränkt addieren und multiplizieren.
- Man sagt, ℕ ist bezüglich der Addition und Multiplikation abgeschlossen.
- Alle anderen Rechenoperationen sind nicht uneingeschränkt durchführbar.
Ganze Zahlen ℤ
Erweiterst du den Zahlenbereich der natürlichen Zahlen mit den negativen Zahlen, hast du die ganzen Zahlen:
- In der Menge der negativen Zahlen sind alle positiven und negativen Zahlen ohne Komma: ℤ={…,-3,-2,-1,0,1,2,3,…}
- Nun kannst du auch uneingeschränkt subtrahieren.
Nachfolgerprinzip: Ist n eine beliebige natürliche Zahl, dann ist n+1 ihr Nachfolger.
Beispiel: Die Zahl n=73 hat den Nachfolger n+1=74
Abgeschlossenheit: Das Ergebnis der Rechnung ist in derselben Menge, hier ℕ.
Beispiel:
- Addierst du zwei natürliche Zahlen, ist die Summe auch eine natürliche Zahl. 4+3=7
- Rechnest du 4:3, ist das Ergebnis keine natürliche Zahl, sondern ein Bruch 43.
Was sind gebrochene und rationale Zahlen?
Gebrochene Zahlen ℚ+
Willst du uneingeschränkt dividieren, brauchst du die Bruchzahlen.
- ℚ+ enthält alle positiven Brüche
- ℚ+={ab∣ a,b sei eine natürliche Zahl und b≠0}
Rationale Zahlen ℚ
Nimmst du die negativen Brüche hinzu, hast du die rationalen Zahlen.
- ℚ={ab∣ a sei eine ganze Zahl ,b sei eine natürliche Zahl und b≠0}
- In ℚ darfst du alle Grundrechenarten uneingeschränkt ausführen.
- ℚ enthält alle positiven und negativen Brüche, sowie alle abbrechenden Dezimalbrüche (z.B. -3,75) und periodischen Dezimalbrüche (z.B. 0,66666…).
Einen Bruch schreibst du allgemein ab.
Der Quotient aus zwei natürlichen Zahlen ist positiv.
Die Division durch Null ist in keinem Zahlenbereich erlaubt, deshalb b≠0.
a kann negativ sein, so kann auch der Quotient negativ sein.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
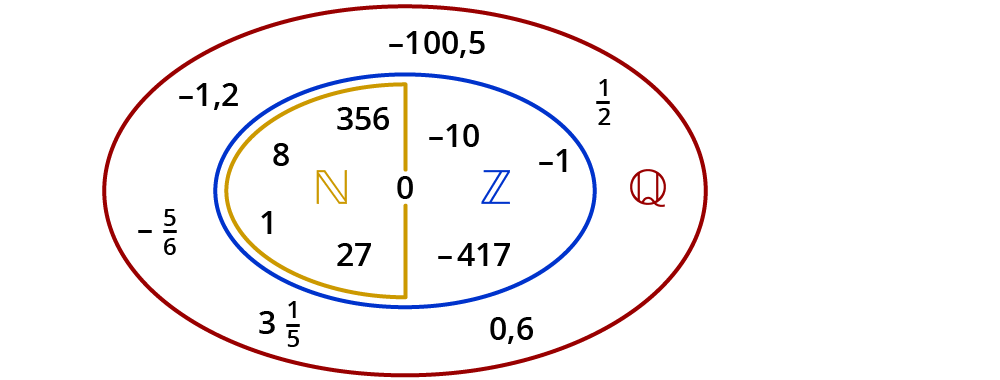
Zahlenbereiche ineinander
Die Zahlenbereiche liegen ineinander.
Zum Beispiel ist die 2 eine natürliche Zahl, eine ganze Zahl und eine rationale Zahl.

kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen