Anwendungsaufgaben mit Zinsrechnung
Zinsen, Zinsen
Anwendungsaufgaben mit Zinsen haben immer mit Sparen oder Krediten zu tun. Allermeistens steht deshalb in den Aufgaben, ob die Zinsen, das Kapital oder der Zinssatz gesucht ist.
Dann wendest du die Formeln an:
Jahreszinsen
Z=K⋅p100
Monatszinsen (für m Monate)
Z=K⋅p100⋅m12
Tageszinsen (für t Tage)
Z=K⋅p100⋅t360
Kapital
K=Z⋅100p mit Jahreszinsen Z
Zinssatz
p=100K⋅Z mit Jahreszinsen Z
Zinseszinsen
Wenn du Zinsen für mehrere Jahre berechnest, liest du genau in der Aufgabenstellung nach, ob die Zinsen mitverzinst werden. Falls ja, bestimmst du den Zinsfaktor q und berechnest die Zinseszinsen.
Die Formel für n Jahre:
Kn=K⋅qn
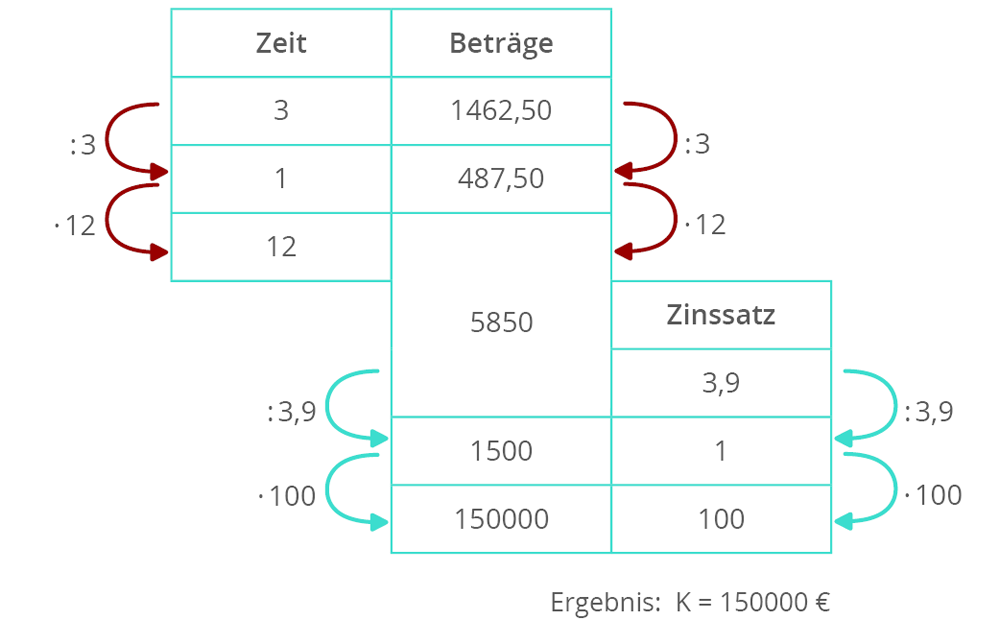
Du kannst auch immer mit dem Dreisatz rechnen. Aber mit der Formel wirst du irgendwann schneller mit dem Rechnen sein.
Verschiedene Angebote
Bei Anwendungsaufgaben geht es oft um Kredite. Es gibt ganz verschiedene Kredite zu ganz verschiedenen Konditionen: Anzahlung, Zinssatz, verschiedene Guthaben, …
Um Kredite vergleichen zu können, rechnest du immer die gesamte Summe aus, die für den Kredit zurückgezahlt werden muss. Dann erst kannst du beurteilen, welcher Kredit das günstigere Angebot ist.
| Angebot 1 | Angebot 2 |
|---|---|
| Sie bekommen: 30000 € Jahreszins: 9,5 % | Sie bekommen: 30000 € Monatsrate: 2500€ Einmalzahlung: 3350 € |
Welches Angebot ist für eine Laufzeit von 1 Jahr günstiger?
Berechne für Angebot 1 und 2, wie hoch die Gesamtkosten sind.
Angebot 1:
Zuerst berechnest du die Zinsen:
Z=30000 €⋅9,5100=2850 €
Addierst du die Zinsen zu den 30000 €, erhältst du die Gesamtkosten:
Kosten=30000 €+2850 €=32850 €
Die Gesamtkosten für Angebot 1 betragen 32850 €.
Angebot 2:
Die Gesamtkosten bestehen aus den 12 Monatsraten und der Einmalzahlung. Deshalb rechnest du
Kosten=12⋅2500 €+3350 €=33350 €.
Die Gesamtkosten betragen 33350 €.
Also ist Angebot 1 günstiger.
Wann gibt es welchen Kredit?
Das sind die häufigsten Kreditarten:
Dispokredit
Wenn dir die Bank das Überziehen deines Girokontos erlaubt, spricht man von einem Dispokredit oder kurz Dispo. Du musst keinen besonderen Vertrag mit der Bank abschließen und bist frei in der Art der Rückzahlung. Dafür sind die Zinsen mit mehr als 10 % sehr hoch. Einen Dispokredit solltest du also möglichst schnell zurückzahlen.
Konsumentenkredit
Möchtest du dir einen Computer kaufen, einen Fernseher oder sogar ein Auto, stellt dir die Bank einen Konsumentenkredit (oder Ratenkredit) zur Verfügung. Hierzu schließt du mit der Bank einen Vertrag ab. In dem Vertrag steht die Rückzahlung in festen Raten. Die Zinsen sind gegenüber dem Dispo wesentlich geringer.
 Bild: fotolia.com
Bild: fotolia.com

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Wann gibt es welchen Kredit?
Immobilienkredit
Für den Kauf eines Hauses oder einer Eigentumswohnung stellt dir die Bank ein Immobiliendarlehen, also einen Immobilienkredit, für einen längeren Zeitraum zur Verfügung. Für die in der Regel sehr hohe Summe verlangt die Bank niedrige Zinsen. Die monatliche Rate ist höher als die zu zahlenden Zinsen, sodass die Schulden in kleinen Raten über bis zu 30 Jahre zurückgezahlt werden.
Pfandleihkredit
Benötigst du sehr kurzfristig Geld und deine Bank möchte dir kein Geld leihen, kannst du einen Gegenstand als Pfand geben und erhältst dafür einen Pfandleihkredit. Neben sehr hohen Zinsen musst du zusätzlich eine Gebühr bezahlen.
 Bild: fotolia.com (Eisenhans)
Bild: fotolia.com (Eisenhans)
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen