Monatszinsen

Frau Klingebiel hat mit einem Sparvertrag auf ihr neues Auto gespart. Da der Vertrag abgelaufen ist, wurde der Sparbetrag von 18.000 € auf ihr Girokonto umgebucht. Geld auf dem Girokonto wird von der Bank nicht verzinst. Das neue Auto wird erst in 4 Monaten geliefert. Für die Zwischenzeit legt Frau Klingebiel ihr Geld auf einem Tagesgeldkonto der Bank an, bei dem sie täglich über ihr Geld verfügen kann. Sie erhält dafür einen Jahreszins von $$p\ = 1,7\ %$$.

Das Geld steht der Bank also nicht ein Jahr lang zur Verfügung, sondern nur 4 Monate.

Wie viel Zinsen bekommt Frau Klingebiel für die 4 Monate?

So löst du die Aufgabe:

Mit dem Dreisatz

Du brauchst zweimal den Dreisatz. Berechne erst die Jahreszinsen und dann die Monatszinsen.

Mit der Formel

Zweimal Dreisatz ist ganz schön viel Rechnerei, oder?

Es geht schneller mit der Formel. Du berechnest den Anteil an den Jahreszinsen.

Beispiel: Für 4 Monate bezahlst du $$4/12$$ der Jahreszinsen. Denn 1 Jahr hat ja 12 Monate.

Allgemein: Für m Monate beträgt der Anteil von den Jahreszinsen $$m/12$$.

$$Z =$$ Jahreszinsen $$* m/12$$,
$$Z = K * p/100 * m/12$$.

Frau Klingebiel rechnet also

$$Z = 18000\ € *1,7/100 * 4/12$$
$$Z = 306\ € * 4/12$$
$$Z = 102\ €$$

Tageszinsen

Herr Kara hat sich eine neue Heizung in sein Haus einbauen lassen und muss dafür 13000 € bezahlen. Da sich die Auszahlung seines Bauspardarlehns um 25 Tage verzögert, überzieht er sein Girokonto um diesen Betrag. Seine Bank berechnet dafür Überziehungszinsen von $$12,4\ %$$ für ein Jahr.

Herr Kara leiht sich das Geld aber nur für 25 Tage.

Wie viel Zinsen muss Herr Kara bezahlen?

So löst du die Aufgabe:

Mit dem Dreisatz

Zur Berechnung der Zinsen wird das Jahr in 360 Tage eingeteilt.

Mit der Formel

Beispiel: Für 25 Tage bezahlst du $$25/360$$ der Jahreszinsen. 1 Jahr wird mit 360 Tagen berechnet.

Allgemein: Für t Tage beträgt der Anteil von den Jahreszinsen $$t/360$$.
$$Z = ($$Jahreszinsen$$)$$ $$* t/360$$,
$$Z = K * p/100 * t/360$$.

Frau Klingebiel rechnet also

$$Z = 13000\ € * 12,4/100 * 25/360$$

$$Z = 1612\ € * 25/360$$

$$Z = 111,94\ €$$

Und andersrum: p berechnen

Frau und Herr Roth benötigen für den Kauf einer neuen Küche zusätzlich 8100 € und leihen sich diesen Betrag bei ihrer Bank. Die Rückzahlung muss erst im neuen Jahr beginnen. Man sagt, sie nehmen dafür einen Konsumentenkredit auf. Die Bank stellt das Geld ab dem 01. August zur Verfügung und berechnet zum Jahresende $$Z = 270\ €$$ Zinsen.

Wie hoch ist der Zinssatz, den die Bank berechnet?

Die 270 € sind die Zinsen für 5 Monate (August bis Dezember). Berechne zunächst die Jahreszinsen.

$$Z($$für 1 Jahr$$) =$$ $$(12\ text{Monate})/(5\ text{Monate}) * 270\ €$$

$$= 648\ €$$.

Berechne damit den Zinssatz
$$p\ = (648 *100)/8100 %$$

$$= 8\ %$$

Mit Dreisatz

Es soll der Zinssatz $$p\ $$ berechnet werden.

Zu einem Kapital von $$K = 300\ €$$ werden nach einem Jahr Zinsen in Höhe von $$Z = 15\ €$$ ausgezahlt.

Die Berechnung mit dem Dreisatz lautet:

Achtung: Bei den blauen Pfeilen rechnet man, wie gewohnt, von oben nach unten. Die orangefarbenen Pfeile machen deutlich, dass die Berechnung von unten nach oben erfolgt. Das Ergebnis steht also rechts in der Mitte.

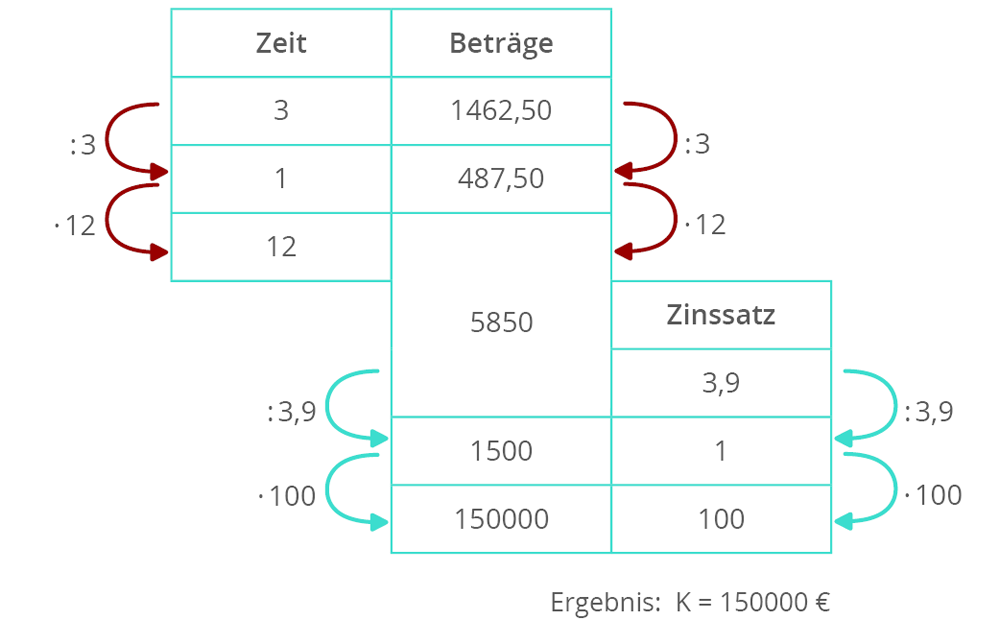
Letztes Beispiel

Familie Bode wohnt zur Miete und möchte sich eine Eigentumswohnung kaufen. Die monatlichen Zinsen sollen nicht höher sein als die derzeitige Miete. In den vergangenen 3 Monaten mussten 1462,50 € an Miete bezahlt werden. Die Hausbank verlangt einen Zinssatz von p = 3,9 %. Familie Bode möchte den höchst möglichen Kreditbetrag wissen.

Zunächst werden die Jahreszinsen berechnet.
$$Z =1462,50\ € 12/3$$ $$Z = 5850\ €$$

Zur Berechnung des Kreditbetrages, also des Kapitals notiert man: $$K = 5850 * (100\ )/(3,9\ )$$

$$K = 150000\ €$$

Bei einem Zinsbetrag $$Z$$, $$m$$ Monaten und dem Zinssatz $$p\ $$ lautet die Formel für das Kapital:

$$K = Z * 12/m * (100\ )/(p\ )$$

Möchte man mit dem Dreisatz rechnen: