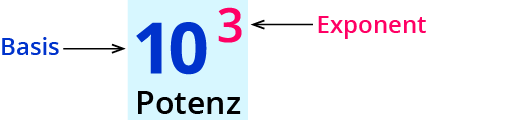Potenzen mit natürlichem Exponenten

Weißt du noch?

`4^5 = 4 * 4 * 4 * 4 * 4`

└───┬────┘

`5`-mal der Faktor `4`

Ein Produkt aus gleichen Faktoren kann als Potenz geschrieben werden.

Weitere Beispiele:

`2^4 = 2 * 2 * 2 * 2`

└──┬───┘

`4`-mal der Faktor `2`

`5^7 = 5 * 5 * 5 * 5 * 5 * 5 * 5`

└─────┬──────┘

`7`-mal der Faktor `5`

Lies: `4` hoch `3`

Negative Basis

Gerader Exponent: Das Ergebnis ist positiv.

Beispiel:

`(-3)^2= 9`

Ungerader Exponent: Das Ergebnis ist negativ.

Beispiel:

`(-3)^3= -27`

Tipps und Tricks

Achtung:

`-3^4 ≠ (-3)^4`, denn

`-3^4= -(3*3*3*3)= -81`

`(-3)^4=(-3)* (-3)* (-3)*(-3)= 81`

Allgemeine Regel:

`-a^n ≠ (-a)^n`

Potenzen mit dem Exponenten `0`

Beispiele:

`3^0=1`

`(-8)^0=1`

`1204^0=1`

Allgemeine Regel:

`a^0=1` für `a ≠ 0`

Potenzen mit dem Formel-Editor

So gibst du in kapiert.de Potenzen mit dem Formel-Editor ein (ab ca. 1:30 im Video):