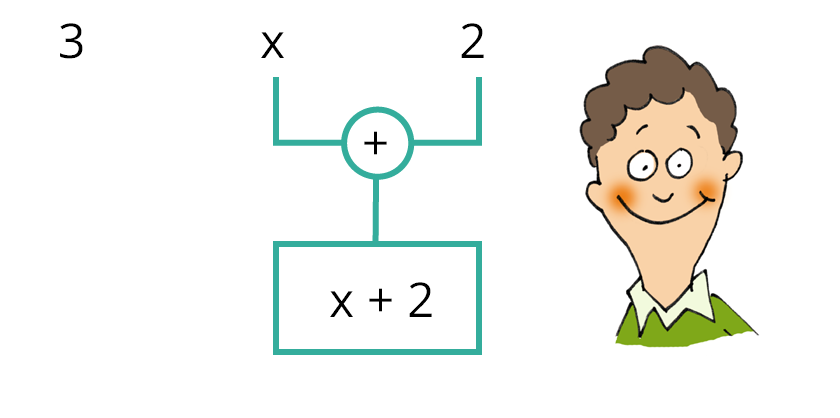Termstrukturen beschreiben
Wozu brauchst du die Struktur von Termen?
Willst du einen Term berechnen, ist es gut, erst seine Struktur zu bestimmen. So erleichterst du dir die Rechnung. Die Struktur eines Terms kannst du an seinem Rechenbaum ablesen.
Beispiel 1: Term ohne Variable
Bestimme die Struktur des Terms 8 : (4 - 2) - 1.
So gehst du vor:
Stelle den Rechenbaum auf. Bestimme dazu die Reihenfolge, in der die Rechenoperationen ausgeführt werden müssen. Nutze dabei die Vorrangregeln.
Als erstes: Klammern (4 - 2) .

Als zweites: Division 8 : (4 - 2).

Als drittes: Subtraktion 8 : (4 - 2) - 1.

Vorrangregeln sind:
- Klammern immer zuerst
- Potenzen ausrechnen
- Punkt- vor Strichrechnung
- Von links nach rechts rechnen
In Wortform lautet der Term:
Dividiere 8 durch die Differenz von 4 und 2 und subtrahiere 1 vom Quotienten.
Beispiel 2: Term mit Variable
Bestimme die Struktur des Terms 3 ⋅ (x+2) .
So gehst du vor:
Stelle den Rechenbaum auf. Bestimme dazu die Reihenfolge, in der die Rechenoperationen ausgeführt werden müssen. Nutze dabei die Vorrangregeln.
Als erstes: Klammern (x+2).

Als zweites: Multipliaktion 3 ⋅ (x+2).

Vorrangregeln sind:
- Klammern immer zuerst
- Potenzen ausrechnen
- Punkt- vor Strichrechnung
- Von links nach rechts rechnen
In Wortform lautet der Term:
Multipliziere 3 mit der Summe von x und 2.
Beispiel 3: Term mit Variable
Bestimme die Struktur des Terms 2 ⋅ x + x : 4 + 5 .
So gehst du vor:
Stelle den Rechenbaum auf. Bestimme dazu die Reihenfolge, in der die Rechenoperationen ausgeführt werden müssen. Nutze dabei die Vorrangregeln.
Als erstes: Multiplikation und Division 2 ⋅ x und x : 4.

Als zweites: Addition 2 ⋅ x + x : 4 .

Als drittes: Addition 2 ⋅ x + x : 4 + 5 .

Vorrangregeln sind:
- Klammern immer zuerst
- Potenzen ausrechnen
- Punkt- vor Strichrechnung
- Von links nach rechts rechnen
In Wortform lautet der Term:
Addiere das Produkt von 2 und x zum Quotienten aus x und 4. Addiere anschließend 5.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Beispiel 4: Term mit Potenzen
Bestimme die Struktur des Terms (x + 1)2.
So gehst du vor:
Stelle den Rechenbaum auf. Bestimme dazu die Reihenfolge, in der die Rechenoperationen ausgeführt werden müssen. Nutze dabei die Vorrangregeln.
Als erstes: Klammern (x+1)

Als zweites: Potenzen (x + 1)2.

r
rr
Vorrangregeln sind:
- Klammern immer zuerst
- Potenzen ausrechnen
- Punkt- vor Strichrechnung
- Von links nach rechts rechnen
r
In Wortform lautet der Term:
Bilde das Quadrat der Summe von x und 1.
Den Typ eines Terms erkennen
Den Typ eines Terms erkennst du an der letzten Rechenoperation im Rechenbaum.
| letzte Rechenoperation | Typ des Terms |
|---|---|
| Addition | Summe |
| Subtraktion | Differenz |
| Multiplikation | Produkt |
| Division | Quotient |
| Potenzierung | Potenz |
Typ erkennen: Beispiel 1 Term ohne Variable
Hier ist nochmal der Rechenbaum des Terms 8 : (4 - 2) - 1. Die letzte Rechenoperation steht in der untersten Verzweigung.

Die letzte Rechenoperation ist eine Subtraktion. Also ist der Typ des Terms eine Differenz.
Du sagst: „Der Term ist eine Differenz“
Typ erkennen: Beispiel 2 Term mit Variable
Hier ist nochmal der Rechenbaum des Terms 3 ⋅ (x+2). Die letzte Rechenoperation steht in der untersten Verzweigung.

Die letzte Rechenoperation ist eine Multipliaktion. Also ist der Typ des Terms eine Produkt.
Du sagst: „Der Term ist ein Produkt“

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Typ erkennen: Beispiel 3 Term mit Variable
Hier ist nochmal der Rechenbaum des Terms 2 ⋅ x + x : 4 + 5. Die letzte Rechenoperation steht in der untersten Verzweigung.

Die letzte Rechenoperation ist eine Addition. Also ist der Typ des Terms eine Summe.
Du sagst: „Der Term ist eine Summe“
Typ erkennen: Beispiel 4 Term mit Potenz
Hier ist nochmal der Rechenbaum des Terms (x + 1)2. Die letzte Rechenoperation steht in der untersten Verzweigung.

Die letzte Rechenoperation ist eine Potenzierung. Also ist der Typ des Terms eine Potenz.
Du sagst: „Der Term ist eine Potenz“
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen