Lineare Gleichungen mit besonderen Lösungsmengen lösen
Sonderfälle beim Gleichungslösen
Wenn du eine Gleichung löst, können diese Sonderfälle vorkommen:
Als Lösungsmenge sind alle rationalen Zahlen möglich. L={ℚ}
Die Gleichung ist bei keiner eingesetzten Zahl richtig. L={ }
0 ist die Lösung der Gleichung. L={0}
1. Als Lösungsmenge sind alle rationalen Zahlen möglich. L={ℚ}
Beispiel:
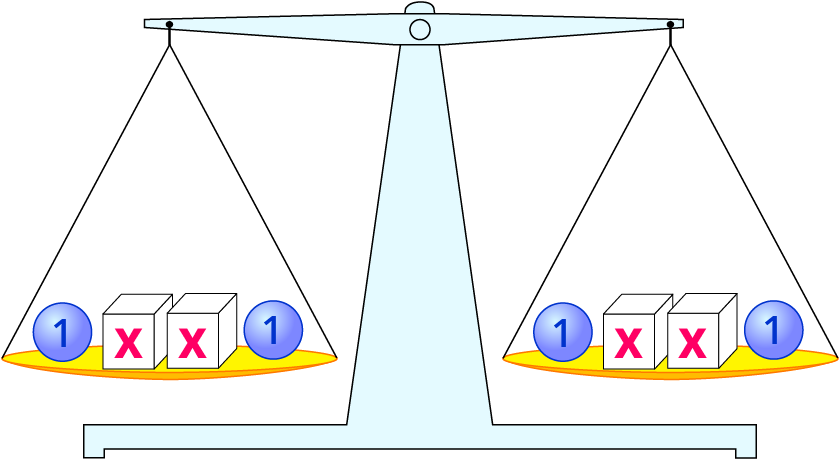
2⋅x+2=2⋅x+2 Du entfernst zwei x-Boxen.
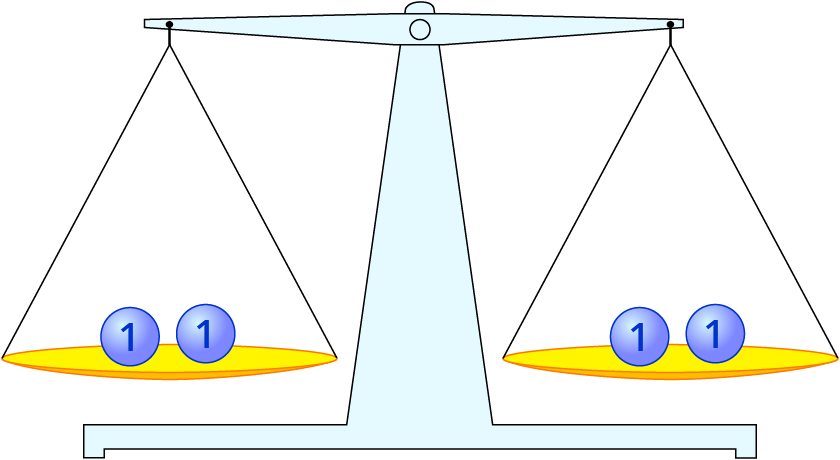
2=2
Es entsteht eine wahre Aussage in der letzten Zeile der aufgelösten Gleichung.
Du kannst jetzt in die x-Box jedes beliebige Gewicht füllen. Da du es auf beiden Seiten der Waagschale tust, bleibt die Waage im Gleichgewicht hängen.
Schreibe die Lösungsmenge so auf: L={ℚ}
ist die unbekannte Gewichtsbox.
steht für 1 kg.
Wenn du noch eine weitere Äquivalenzumformung durchführst, erhälst du 0=0.
2. Die Gleichung ist bei keiner eingesetzten Zahl richtig. L={ }
Beispiel:
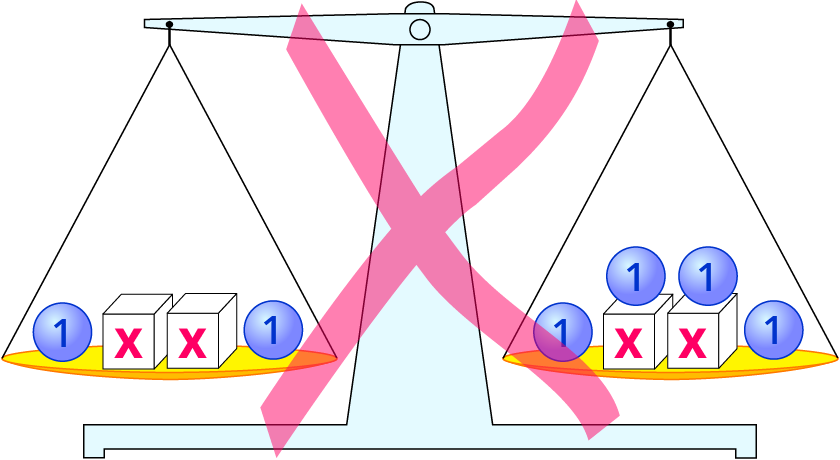
2⋅x+2=2⋅x+4 Du entfernst zwei x-Boxen.
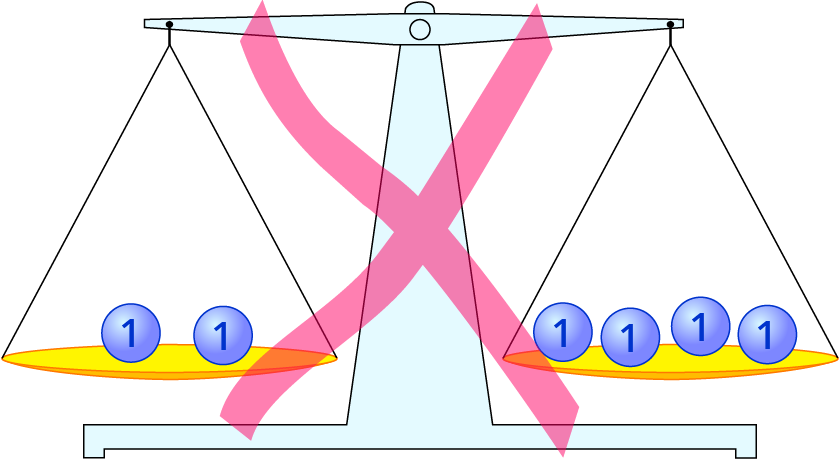
2=4 Das ist eine falsche Aussage.
Die Gleichung ist nicht lösbar. Das heißt die Lösungsmenge ist leer.
Schreibe die Lösungsmenge so auf: L={ }
Zusammenfassung der beiden Sonderfälle:
Immer, wenn bei der Gleichung durch eine zugelassene Umformung das xwegfällt, hat die Gleichung
- entweder keine Lösung L={ }
- oder unendlich viele Lösungen L={ℚ}.
Das Waage-Modell ist durchgestrichen, weil die Waage nicht im Gleichgewicht hängt.
3. 0 ist die Lösung der Gleichung.
L={0}
Beispiel:
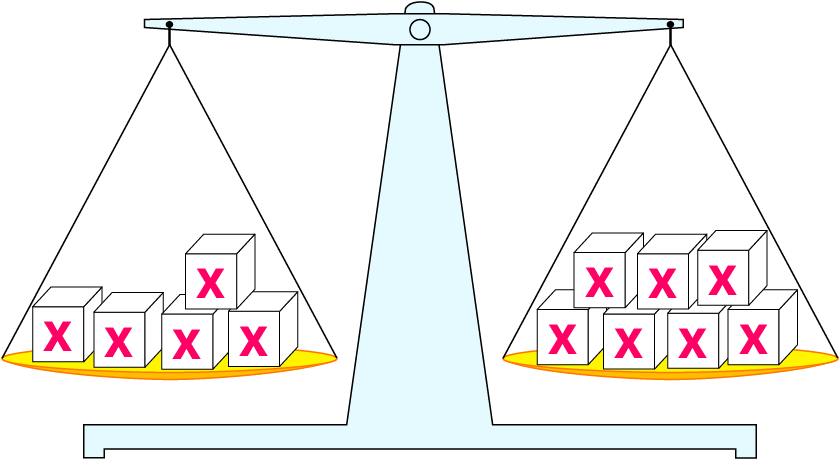
5⋅x=7⋅x ∣-7⋅x
-2⋅x=0 ∣:(-2)
x=0
L={0}
Wenn jede x-Box 0 kg wiegt, hängt die Waage im Gleichgewicht.
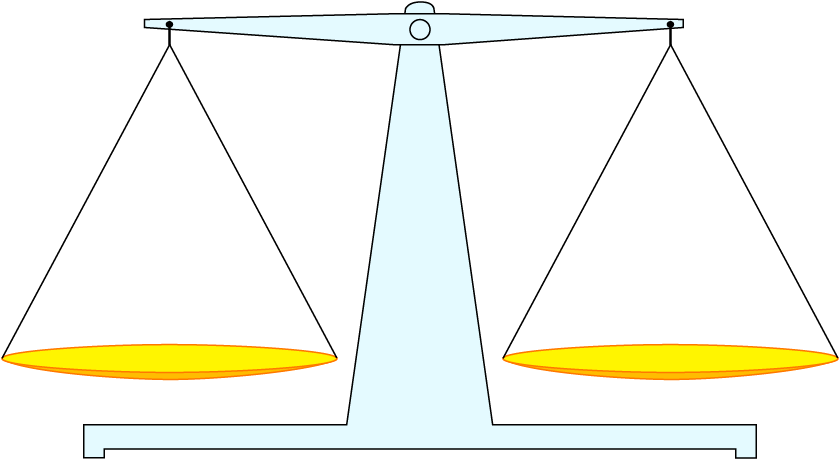
Diese Umformung ist nicht zulässig:
5·x=7·x |x
5=7
Hier würdest du davon ausgehen, dass x nicht 0 ist, denn durch 0 kannst du nicht dividieren. Die 0 ist aber gerade die Lösung.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen
