Lineare Gleichungen lösen 1
Das Waage-Modell
So löst du lineare Gleichungen mit dem Waagemodell:
Gleichungen mit dem Waage-Modell lösen
Bei einer Gleichung hast du immer die eckigen Gewichtsstücke und die Kugeln. Statt „eckiges Gewichtsstück“ kannst du auch x-Box sagen. Von den x-Boxen kennst du das Gewicht noch nicht.
Die Boxen und Kugeln werden entsprechend einer Gleichung auf zwei Waagschalen verteilt.
Die Waage soll immer im Gleichgewicht bleiben.
Ziel: Wie schwer ist eine x-Box?
Beispiel: 2⋅x+5=11
1. Fülle die Waage entsprechend der Gleichung.
2⋅x+5=11
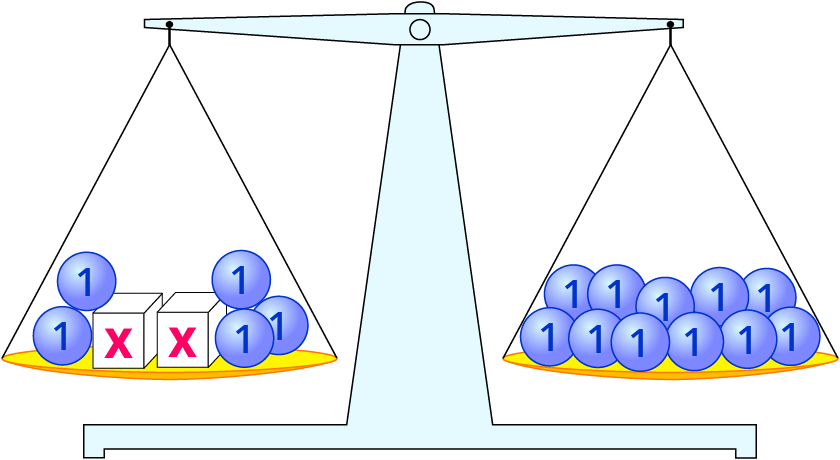
2. Nimm aus beiden Waagschalen fünf Kugeln weg.
Die Waage bleibe im Gleichgewicht.
2⋅x=6
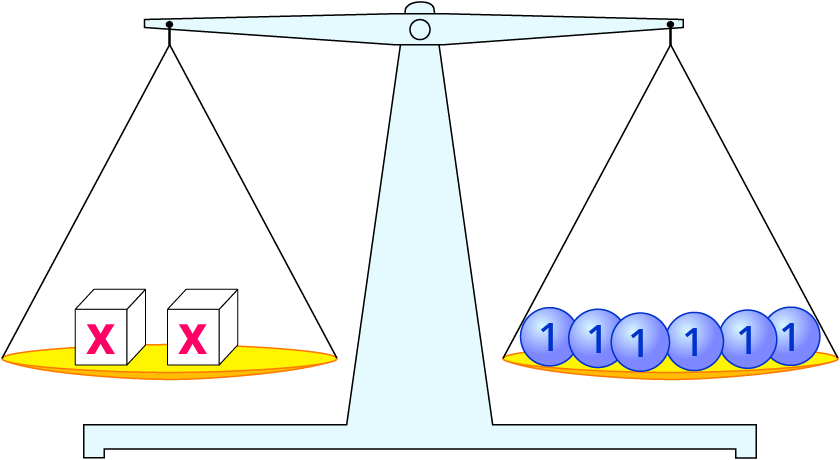
3. Da du wissen willst, wie schwer eine Box ist, nimmst du auf jeder Seite den zweiten Teil (geteilt durch 2).
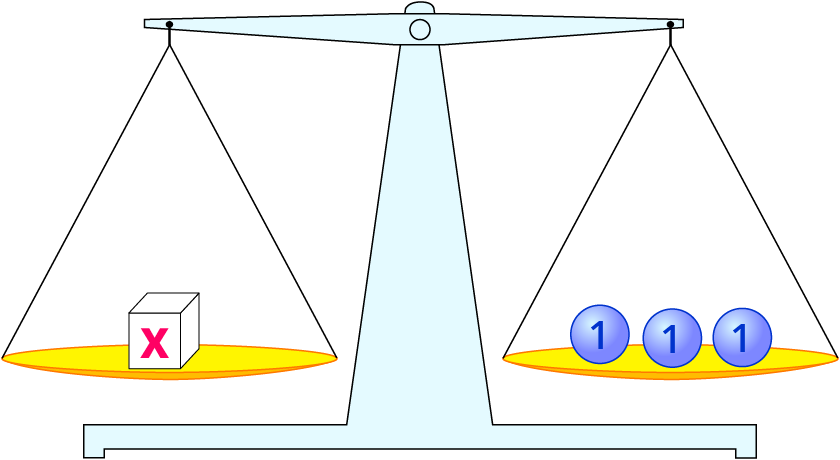
x=3 ist die Lösung der Gleichung.
L={3} ist die Lösungsmenge.
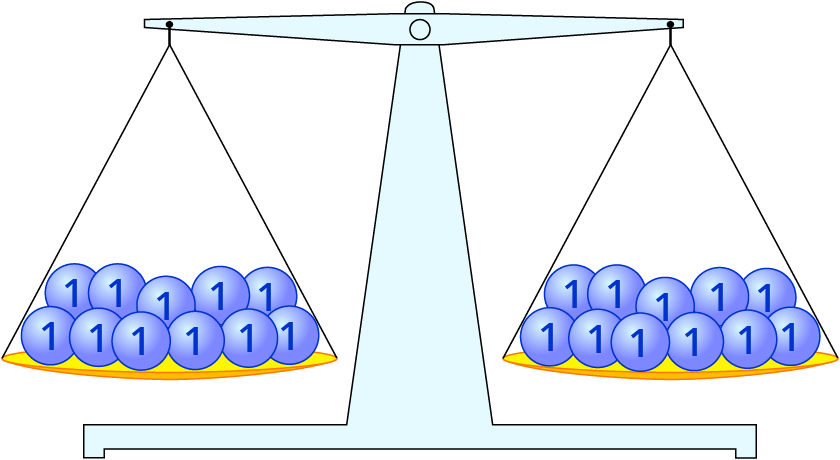
Probe
Wenn du wissen willst, ob eine Box tatsächlich 3 kg wiegt, kannst du 3 kg für jede Box einsetzen.

x-Boxen sind alle gleich schwer

1 - kg - Kugeln
Gleichungen durch Äquivalenzumformung lösen
Irgendwann brauchst du das Waage-Modell gar nicht mehr und rechnest einfach so:
2⋅x+5=11 ∣-5
Du rechnest zuerst auf beiden Seiten der Gleichung - 5.
2⋅x+5-5=11-5
2⋅x=6 ∣:2
2:2⋅x=6:2
x=3
L={3}
In der Kurzfassung lässt du die blauen Schritte weg.
Probe:
Setze 3 für x ein. Steht auf beiden Seiten der Gleichung dasselbe?
2 ⋅ 3 + 5=11
11=11 Ja!
Du formst eine Gleichung um, indem du auf beiden Seiten
- dieselbe Zahl addierst oder subtrahierst
- mit derselben Zahl multiplizierst oder dividierst (die 0 ist dabei ausgenommen)
Denke immer daran, dass du auf beiden Seiten der Gleichung dasselbe rechnest.
Das sind Äquivalenzumformungen, sie ändern nichts an der Lösung der Gleichung.
Der Strich ∣ ist wie die Regieanweisung: „Tu auf beiden Seiten dasselbe!“ zu verstehen. Die Lösung der Gleichung wird dann nicht verändert.
Schwierigere Gleichungen
Manche Gleichungen haben fiese Minuszeichen. Diese Gleichungen löst du so:
-3⋅x–7=20 ∣+7
-3⋅x–7+7=20+7
-3⋅x=27 ∣:(-3)
-3:(-3)⋅x=27:(-3)
x=-9
L={-9}
Mit etwas Übung kannst du die blauen Schritte weglassen.
Die Probe führst du hier rechnerisch durch. Setze (-9) für x ein.
Steht auf beiden Seiten der Gleichung wirklich dasselbe?
-3 ⋅ (-9) -7=20
27-7=20
20=20 JA!
Kennst du schon das Zahlenstrahl-Modell?
Bei dem Zahlenstrahl-Modell trägst du die Gleichung wie im Bild ein.
Beispiel: 2⋅x+5=11
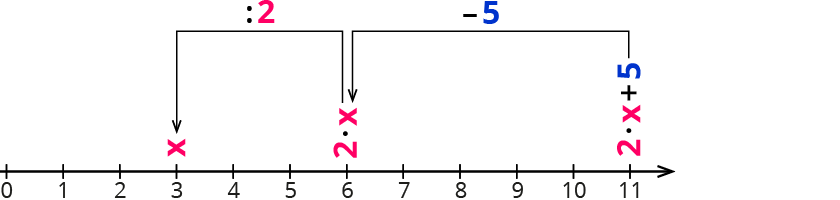
- 11 ist der Ausgangswert deiner Gleichung.
- Wenn du - 5 rechnest, wandert die Gleichung um 5 Schritte nach links.
- Wenn du durch 2 teilst, hast du x allein stehen.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen


