Lineare Gleichungen lösen 2
Das Waage-Modell
Das Waage-Modell kannst du für das Lösen von Gleichungen durch Umformen benutzen. Es funktioniert auch, wenn x auf beiden Seiten der Gleichung auftaucht.
Du hast Kugeln, die alle 1 kg wiegen. Außerdem hast du gleichschwere x-Boxen. Von ihnen kennst du das Gewicht noch nicht.
Du verteilst Boxen und Kugeln entsprechend einer Gleichung auf zwei Waagschalen.
Die Waage soll immer im Gleichgewicht bleiben.
Ziel: Wie schwer ist eine x-Box?
Beispiel: 6⋅x+3=2⋅x+11
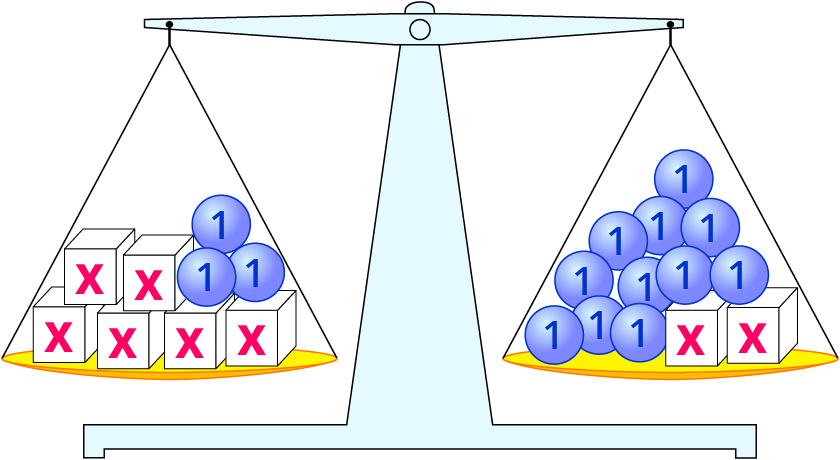
links: 6 x-Boxen, 3 Kugeln
rechts: 2 x-Boxen, 11 Kugeln
Bisher: x auf einer Seite
2x+3=5
Jetzt: x auf beiden Seiten
7x+5=2x-4

x-Boxen sind alle gleich schwer

1 - kg - Kugeln
Jetzt wird umgeformt
6⋅x+3=2⋅x+11 
6⋅x+3=2⋅x+11 ∣-2⋅x
Du nimmst aus beiden Waagschalen zwei x-Boxen weg. Die Waage hängt weiter im Gleichgewicht.
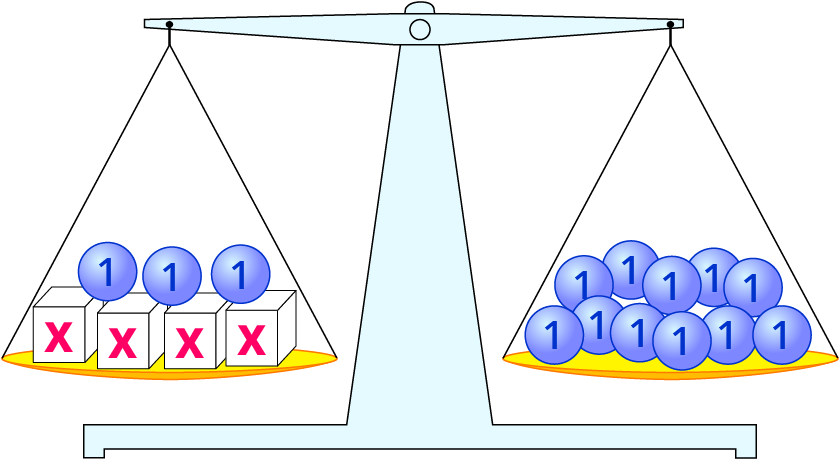
Ab jetzt verfährst du, wie bekannt und entfernst drei Kugeln auf jeder Seite.
4⋅x+3=11 ∣-3
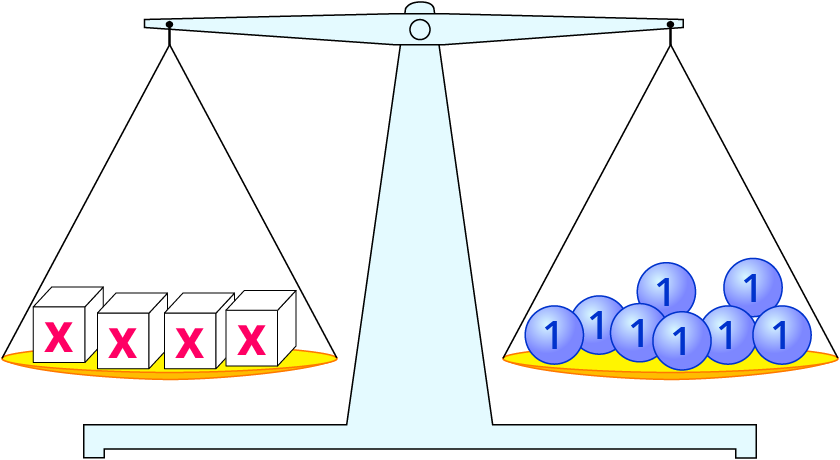
Du bildest auf jeder Seite den vierten Teil, rechnest also : 4.
4⋅x=8 ∣ :4
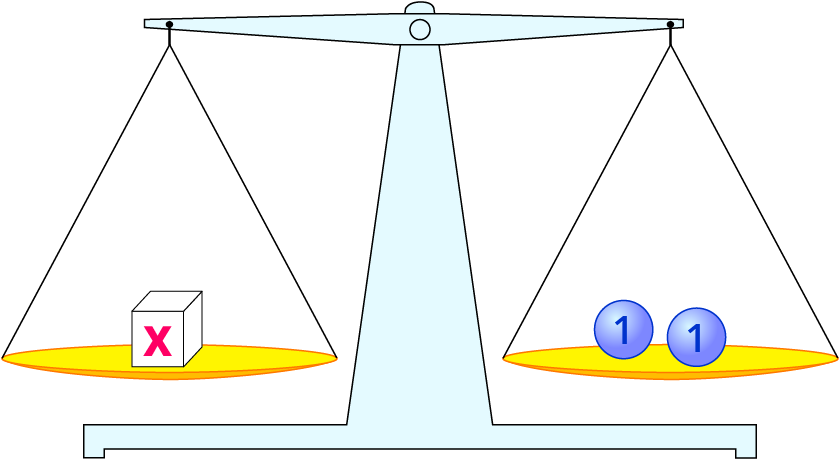
Eine x-Box wiegt 2 kg.
x=2
L={2}
Die Probe im Waage-Modell machen
Zum Schluss machst du immer die Probe, ob dein Ergebnis stimmt.
6⋅x+3=2⋅x+11

6⋅2+3=2⋅2+11
Wenn du für jede x-Box drei Kugeln auf die Waage legst, sind auf jeder Seite der Waage 15 Kugeln.
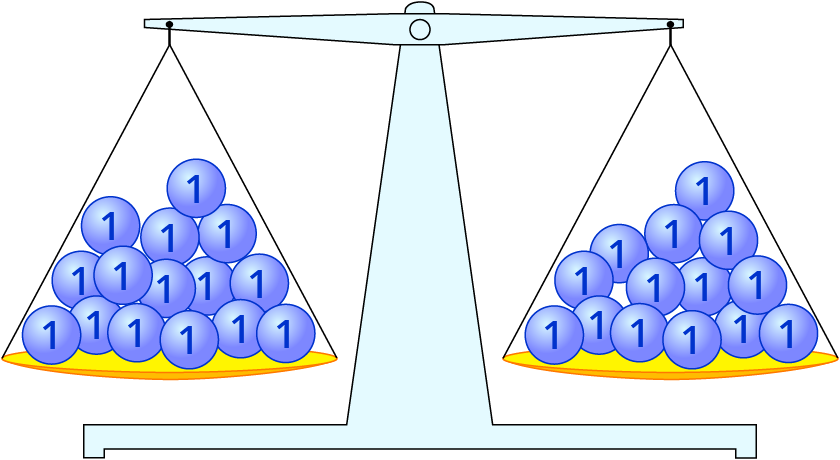
15=15
Ohne Waage-Modell Gleichungen lösen
So löst du Gleichungen mit x auf beiden Seiten rechnerisch:
6⋅x+3=2⋅x+11 ∣-2⋅x
6⋅x-2⋅x+3=2⋅x-2⋅x+11
4⋅x+3=11 ∣-3
4⋅x+3-3=11-3
4⋅x=8 ∣:4
4⋅x:4=8:4
x=2
L={2}
Probe:
Überall dort, wo x steht, setzt du die Lösung 2 ein.
6 ⋅ x +3=2 ⋅ x + 11
6 ⋅ 2 +3=2 ⋅ 2 + 11
12+3=4+11
15=15 Ja, 2 löst die Gleichung.
Der Strich ∣ ist die Regieanweisung: „Tu auf beiden Seiten dasselbe!“.
Die blauen Zwischenschritte kannst du später weglassen.
Schwierigere Gleichungen
Bei langen Gleichungen ist es leichter, wenn du zuerst gleiches zusammenfasst.
Beispiel:
4x+6+7x+1=16x+3-9⋅x ∣ zusammenfassen
11x+7=7x+3 ∣-7⋅x
4x+7=3 ∣-7
4x=-4 ∣ :4
x=-1
L={-1}
Probe:
Überall dort, wo x steht, setzt du die Lösung (-1) ein.
4 ⋅ x + 6 + 7 ⋅ x + 1=16 ⋅ x + 3 - 9 ⋅ x
4 ⋅ (-1) + 6 + 7 ⋅ (-1) + 1=16 ⋅ (-1) + 3 - 9 ⋅ (-1)
-4+6-7+1=-16+3+9
-11+7=-16+12
-4=-4 Ja, (-1) passt.
Den Malpunkt ⋅ zwischen Zahl und Variable kannst du weglassen.
Rechenregeln für die Multiplikation mit negativen Zahlen
-⋅-=+
-⋅+=-
Was machst du, wenn die Gleichung eine Klammer hat?
Löse immer zuerst die Klammer auf.
Beispiel 1:
2⋅(-5+x)=2 ∣ Klammer auflösen
-10+2x=2 ∣+10
2x=12 ∣:2
x=6
L={6}
Probe:
Setze für x die Lösung 6 ein.
2⋅(-5 + 6 )=2
2=2
Beispiel 2:
-3⋅(x-6)+6x=-3+6x ∣ Klammer auflösen
-3x+18+6x=-3+6x ∣ zusammenfassen
3x+18=-3+6x ∣-6x
-3x+18=-3 ∣-18
-3x=-21 ∣:(-3)
x=7
L={7}
Probe:
Setze für x die Lösung 7 ein.
-3 ⋅ (7 - 6) + 6 ⋅ 7 =-3 + 6 ⋅ 7
-3⋅1+42=-3+42
39=39
Um die Gleichung zu vereinfachen, kannst du auch als erstes die Äquivalenzumformung ∣ -6⋅x rechnen.
Gleichungen mit dem Formel-Editor
So gibst du Zahlen und Variablen in kapiert.de ein:
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen