Gleichungssysteme grafisch lösen
Anwendung für das grafische Lösen von Gleichungssystemen
Aufgabe:
Ein Elektrizitätsunternehmen bietet zwei Tarife an.
| Tarif | „Basis“ | „Kompakt“ |
|---|---|---|
| Grundpreis je Monat | 4,00 € | 8,00 € |
| Preis je kWh | 0,20 € | 0,10 € |
Herr Richter verbraucht monatlich 50 kWh. Welcher Tarif ist für ihn günstiger?
Lösung:
Die Lösung erfolgt in zwei Schritten:
- Aufstellen der linearen Gleichungen mit zwei Variablen
- Zeichnen der Grafen in ein Koordinatensystem
kWh: Kilowattstunde
1. Aufstellen der linearen Gleichungen mit zwei Variablen
Lege zuerst die Variablen fest:
x : Anzahl der pro Monat verbrauchten kWh
y : Kosten pro Monat in €
Gleichung für Tarif Basis:
Pro kWh sind 0,2 € zu zahlen, für x kWh also 0,2⋅x.
Dazu kommt pro Monat ein Grundpreis von 4 €.
Zusammen entstehen pro Monat Kosten von
y=0,2⋅x+4 (I).
Gleichung für Tarif Kompakt:
Pro kWh sind 0,1 € zu zahlen, für x kWh also 0,1⋅x.
Dazu kommt pro Monat ein Grundpreis von 8 €.
Zusammen entstehen pro Monat Kosten von
y=0,1⋅x+8 (II).
y=0,2⋅x+4 (I) und
y=0,1⋅x+8 (II) sind lineare Funktionsgleichungen der allgemeinen Form y=m⋅x+b.
Diese Form heißt Normalform.
Dabei gelten:
(I) Steigung m = 0,2 und
Achsenabschnitt b = 4
(II) Steigung m = 0,1 und
Achsenabschnitt b = 8
2. Zeichnen der Grafen in ein Koordinatensystem
Zur Lösung der Aufgabe suchst du die Zahlenpaare (x|y), die die Gleichungen (I) und (II) erfüllen.
Beide Gleichungen bilden ein lineares Gleichungssystem.
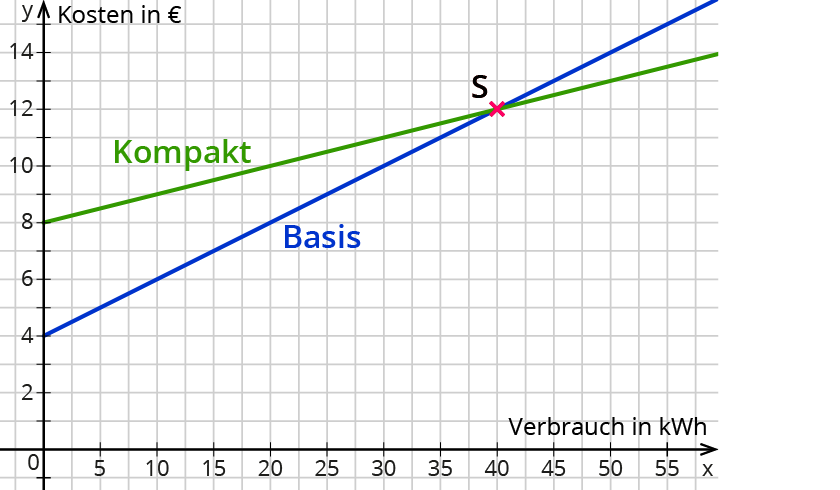
Zeichne die beiden Graphen:

Folgendes kannst du aus den Graphen und ihrem Schnittpunkt ablesen:
Bis zu einem monatlichen Verbrauch von 40 kWh ist Tarif Basis günstiger. Liegt der Verbrauch über 40 kWh pro Monat, ist der Tarif Kompakt günstiger.
Herr Richter sollte Tarif Kompakt wählen.
Oft interessiert dich neben dem Verlauf der Geraden ihr Schnittpunkt S.
Schreibweise für ein lineares Gleichungssystem aus zwei Gleichungen mit zwei Variablen:
|y=0,2x+4y=0,1x+8|

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Verlauf der Geraden
Der Verlauf der Geraden, deren Funktionsgleichungen aus einem gegebenen linearen Gleichungssystem ergeben, hängt von deren Steigungen und y-Achsenabschnitten ab.
Es gibt drei verschiedene Möglichkeiten für die Lösung
eines Gleichungssystems:
- Genau eine Lösung
- Keine Lösung
- Unendlich viele Lösungen
Funktionsgleichung in Normalform:
y= m⋅x+b mit m als Steigung und b als y-Achsenabschnitt oder kurz als Achsenabschnitt.
1. Möglichkeit: Genau eine Lösung

Die Geraden (I) und (II) haben unterschiedliche Steigungen.
Sie schneiden sich in einem Punkt.
Das zugehörige Gleichungssystem hat genau eine Lösung.
Lineares Gleichungssystem:
|y=-x+5y=2x+2|
Ablesen der Lösung:
x = 1 und y = 4
Lösungsmenge:
L = {(1|4)}
Punktprobe:
(I) -1+5=4 und (II) 2⋅1+2=4
Die Geraden (I) und (II) haben unterschiedliche Steigungen.
Sie schneiden sich in einem Punkt.
Das zugehörige Gleichungssystem hat genau eine Lösung.
2. Möglichkeit: Keine Lösung

Die Geraden (I) und (II) haben die gleiche Steigung, aber unterschiedliche Achsenabschnitte. Sie verlaufen parallel zueinander und schneiden sich nicht.
Das zugehörige Gleichungssystem hat keine Lösung.
Lineares Gleichungssystem:
|y=0,5x+1y=0,5x+2|
keine Lösung:
Die Lösungsmenge ist leer:
L = { }

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
3. Möglichkeit: Unendlich viele Lösungen

Die Geraden (I) und (II) haben gleiche Steigung und gleiche Achsenabschnitte. Sie fallen zusammen.
Das zugehörige Gleichungssystem hat unendlich viele Lösungen und besteht aus allen Zahlenpaaren, die die Geradengleichung erfüllen.
Lineares Gleichungssystem:
|y=-0,5x+4y=-0,5x+4|
Lösung:
L = {(x|y) | y = -0,5x + 4 }
gelesen:
alle Zahlenpaare (x|y) mit der Eigenschaft y = -0,5x + 4
Die Geraden (I) und (II) haben gleiche Steigung und gleiche
Achsenabschnitte. Sie fallen zusammen.
Das zugehörige Gleichungssystem hat unendlich viele
Lösungen und besteht aus allen Zahlenpaaren, die die
Geradengleichung erfüllen.
Ohne Zeichnen die Anzahl der Lösungen bestimmen
Du kannst schon an den Steigungen und Achsenabschnitten erkennen, ob sich die Geraden eines linearen Gleichungssystems schneiden, ob sie parallel verlaufen oder ob sie identisch sind.
Lösung:
Die Lösung erfolgt in zwei Schritten:
Forme die Gleichungen in die Normalform y = m⋅x + b um.
Vergleiche m und b:
- Werte für m unterschiedlich:
Geraden schneiden sich - es gibt genau eine Lösung
Beispiel: |y=-x+5y=2x+2|
- Werte für m gleich und für b unterschiedlich:
Geraden verlaufen parallel - Lösungsmenge ist leer
Beispiel: |y=0,5x+1y=0,5x+2|
- Werte für m und b gleich:
Geraden identisch - es gibt unendliche viele Lösungen
Beispiel: |y=-0,5x+4y=-0,5x+4|
Funktionsgleichung in Normalform:
y= m⋅ x + b
m als Steigung
b als y-Achsenabschnitt oder kurz als Achsenabschnitt.
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen