Extremwerte quadratischer Terme ablesen
Extremwerte
Ein quadratischer Term besitzt einen kleinsten oder größten Termwert. Diese so genannten Extremwerte werden Minimum bzw. Maximum genannt.
Beispiel für einen quadratischen Term mit einem Minimum
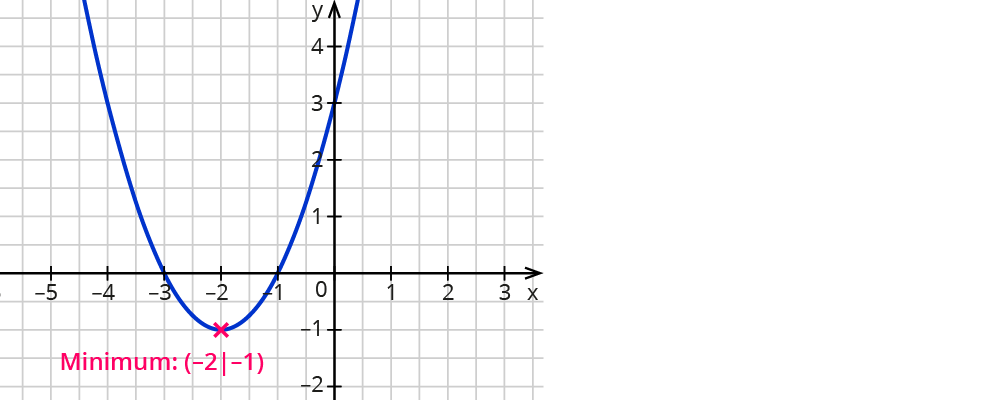
Es liegt folgender Term vor: T(x)=(x+2)2-1.
Hier eine Wertetabelle für den Term:
| x | -4 | -3 | -2 | -1 | 0 | 1 |
| T(x) | 3 | 0 | -1 | 0 | 3 | 8 |
Der Graf hat folgendes Aussehen:

Das Minimum wird dann in folgender Form angegeben:
Tmin(-2∣-1).
Man sagt auch Tmin=-1 für x=-2.
Vergleiche das Minimum mit dem gegebenen Term. Aus der Darstellung kannst Du genau ablesen, um welchen Extremwert es sich handelt:
Vor der Klammer steht ein Pluszeichen. Hier liegt ein Minimum vor, denn für jedes x liefert das Quadrieren Werte, die größer oder gleich Null sind.
Wann wird die Klammer genau 0? Für x+2=0, also x=-2.
Der Funktionswert des Minimums entspricht der Zahl hinter der binomischen Formel, denn
T(-2)=02-1=-1 und somit Tmin=-1.
Beispiel für einen quadratischen Term mit einem Maximum
Gegebener Term: T(x)=-2(x-1)2+3
Wertetabelle:
| x | -1 | 0 | 1 | 2 | 3 |
| T(x) | -5 | 1 | 3 | 1 | -5 |
Die Abbildung zeigt die grafische Darstellung.
Bestimmung des Maximums
Auch hier kannst Du den Extremwert direkt ablesen:
Vor der Klammer steht ein Minuszeichen. Es liegt ein Maximum vor, denn die quadrierten Werte werden durch das Minus alle kleiner oder gleich Null.
Wann wird die Klammer genau 0? Für x-1=0, also x=1.
Den Funktionswert gibt die Zahl hinter der binomischen Formel an: Tmax=3.
Zusammenfassend kannst Du sagen:
Der Term T(x)=-2(x-1)2+3 hat als Extremwert ein Maximum Tmax=3 für x=1.
Die Koordinaten sind Tmax(1∣3).
Marginalspalte

Das Schema lässt sich dann anwenden, wenn ein quadratischer Term als binomische Formel vorliegt. Wenn dies nicht der Fall ist, wird der Term mit der quadratischen Ergänzung umgeformt.
Extremwert eines quadratischen Terms
Was ist mit T(x)=3x2-12x+7?
Hier musst Du den Term zunächst mit einer binomischen Formel umwandeln, um die Extremwerte ablesen zu können.
Termumwandlung
T(x)=3x2-12x+7
1. Vorfaktor ausklammern
T(x)=3[x2-4x]+7
2. Binomische Formel erkennen und quadratische Ergänzung (hier: +4) addieren und subtrahieren:
T(x)=3[x2-4x+4-4]+7
3. Mit binomischer Formel umformen:
T(x)=3[(x-2)2-4]+7
4. Vereinfachen:
T(x)=3(x-2)2-12+7=3(x-2)2-5
Extremwert ablesen
Jetzt kannst Du den Extremwert einfach ablesen:
Der Term T(x)=3x2-12x+7=3(x-2)2-5
hat als Extremwert ein Minimum Tmin=-5 für x=2.
Die Koordinaten sind Tmin(2∣-5).

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Zusammenfassung
Die allgemeine Form eines quadratischen Terms in der
Darstellung mit einer binomischen Formel lautet
T(x)=a(x-b)2+c.
Extremwertbestimmung
In dieser allgemeinen Formel kannst Du den Extremwert sofort angeben:
Ist a>0, so hat der Term
T(x) ein Minimum Tmin=c für x=b.
Die Koordinaten sind Tmin(b∣c).
Ist a<0, so hat der Term
T(x) ein Maximum Tmax=c für x=b.
Die Koordinaten sind Tmax(b∣c).
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen