Nullstellen quadratischer Terme erkennen
Was ist ein quadratischer Term?
| Grad | Bezeichnung | Beispiel |
|---|---|---|
| 0 | konstanter Term | 7 |
| 1 | linearer Term | 2x+3 |
| 2 | quadratischer Term | x2-3x |
Die Tabelle zeigt ein Beispiel für einen quadratischen Term. Der Begriff quadratisch bezieht sich auf den höchsten Exponenten einer Variablen - hier die 2 in x2-3x.
Oft wird in diesem Zusammenhang auch der Begriff Grad der jeweiligen Variablen gebraucht.
So ein quadratischer Term ist manchmal nicht so einfach zu erkennen.
Sieh dir den Term (x+1)(x-1) an.
Du wirst bestimmt sagen, dass es doch klar ist! Da steckt doch die dritte binomische Formel hinter: (x+1)(x-1)=x2-1 und schon haben wir den quadratischen Term.
Was ist eine Nullstelle?
Dieser Begriff hat zwei Bedeutungen, die aber miteinander zusammenhängen: eine algebraische und eine geometrische Bedeutung.
Zunächst zur algebraischen Bedeutung.
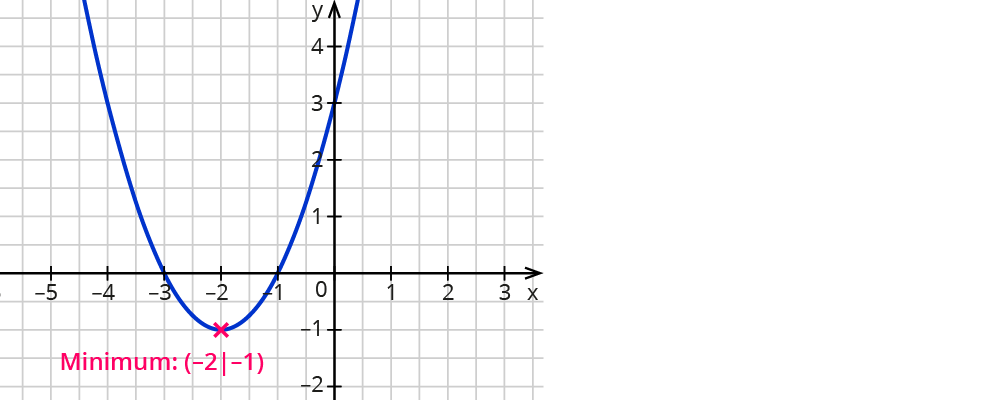
Betrachte das Beispiel x2-2x und fertige für diesen quadratischen Term eine kleine Wertetabelle an:
Überall dort, wo für die Variable x der Term x2-2x den Wert 0 annimmt, liegt eine Nullstelle vor.
Nun zur geometrischen Bedeutung.

Betrachte den Graphen, der zum obigen Term gehört. Du erkennst bestimmt die verschobene Normalparabel.
Geometrisch liegen Nullstellen an den Stellen vor, wo der Graph des Terms mit der x-Achse gemeinsame Punkte aufweist.
Wie werden Nullstellen berechnet?
Denke noch einmal an die Wertetabelle, die für den quadratischen Term x2-2x aufgestellt wurde.
x2-2x=0.
Mit anderen Worten: Es muss die Gleichung x2-2x=0 nach x aufgelöst werden.
Erinnerst du dich noch an die Regeln für Termumformungen? Denkst du konkret an das Distributivgesetz, kannst du einfach x ausklammern: x2-2x=0⇒x(x-2)=0.
Jetzt kannst du einen Satz anwenden, der für ein Produkt gilt, das den Wert 0 haben soll.
Ein Produkt ist genau dann 0, wenn mindestens
einer der Faktoren gleich 0 ist.
Für dieses Produkt ergibt sich also x=0 oder x=2. Damit bekommst du genau die Werte der Nullstellen!
So können auch ganz allgemein die Nullstellen quadratischer Terme ermittelt werden.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Bestimmen von Nullstellen
Nun liegt eine andere Form von Gleichungen vor, deren Lösungen und damit die Nullstellen ermittelt werden sollen.
Ein Beispiel: (x+1)(x-2)=0.
Die grafische Darstellung zeigt dir sofort die Nullstellen.
Wie ist das mit der Berechnung?

Die Methode mit dem Ausklammern funktioniert jetzt nicht - aber die Erklärung über die Null als Ergebnis einer Multiplikation.
(x+1)⋅(x-2)=0 wird nur dann 0, wenn einer der Faktoren 0 wird.
Also muss gelten
(x+1)=0 oder (x-2)=0 und weiter
x=-1 oder x=2.
Du kannst das Ergebnis als Lösungsmenge schreiben:
Die Gleichung (x+1)⋅(x-2)=0 hat die Lösungsmenge L={-1;2}.
Die dritte binomische Formel hilft weiter …
Du erinnerst dich bestimmt:
(a+b)⋅(a-b)=a2-b2 .
Wie hängt diese Formel mit dem Erkennen von Nullstellen zusammen?
In den beiden Beispiele für quadratische Terme konntest du bisher immer ausnutzen, dass die Terme als Produkt vorlagen:
x2-2x=x(x-2)=0 und (x+1)(x-2)=0.
Was machst du nun bei x2-16=0?
Hier kommt die dritte binomische Formel ins Spiel.
x2-16=0 lässt sich anders schreiben: x2-16=x2-42.
Vergleiche jetzt mit der 3. binomischen Formel!
Es folgt für die Berechnung der Nullstellen:
x2-16=0 ergibt (x+4)⋅(x-4)=0 und damit mit der bekannten Erklärung über die 0 als Ergebnis einer Multiplikation als Lösung:
L={-4;4}.
Die Probe …
Zur vollständigen Ermittlung von Nullstellen eines quadratischen Terms gehört natürlich eine Probe, auch wenn sie oft weggelassen wird.
Beispiel mit Probe
Bestimme die Lösungsmenge von (x-7)⋅(x+3)=0.
Du weißt schon, dass die Multiplikation der beiden Faktoren nur dann 0 sein kann, wenn mindestens einer der Faktoren 0 ist.
Es muss also gelten: (x-7)=0 oder (x+3)=0. Damit folgt
x-7=0⇔x=7 oder x+3=0⇔x=-3.
Vor dem Antwortsatz mit der Angabe der Lösungsmenge ist die Probe durchzuführen. Dazu setzt du die berechneten Zahlen einfach in die Ausgangsgleichung ein. Ergibt sich eine wahre Aussage, so ist die betreffende Zahl tatsächlich eine Lösung.
Probe für die Zahl 7:
(7-7)⋅(7+3)=0⇔0⋅10=0⇔0=0.
Es ergibt sich eine wahre Aussage.
Probe für die Zahl -3:
(-3-7)⋅(-3+3)=0⇔-10⋅0=0⇔0=0.
Es ergibt sich wieder eine wahre Aussage.
Nun kann der Antwortsatz formuliert werden:
Die Gleichung (x-7)⋅(x+3)=0 hat die Lösungsmenge L={-3;7}.

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen