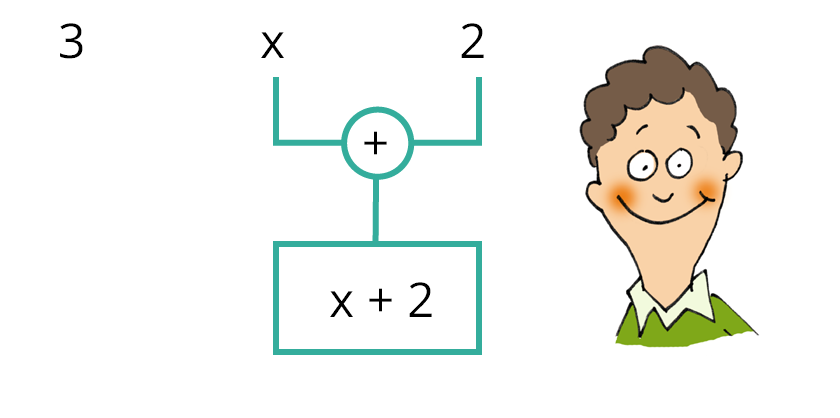Terme aufstellen
So sehen Terme aus
Terme sind sinnvolle Zusammensetzungen von Zahlen, Variablen und Rechenzeichen.
Beispiele für Terme:
(5+3) -56
x+3
5
-2⋅x
12
Terme sind Rechenwege
Terme sind Rechenwege, mit denen du Situationen aus dem Alltag beschreiben kannst.
Beispiel: Arne hat x Bücher. Er kauft sich 3 neue. Wie viele Bücher hat Arne? Stelle einen Term auf.
Antwort:x + 3
Diesen Ausdruck brauchst du nicht ausrechnen, da x keinen festen Wert hat.
Der Term x + 3 gibt nur den Rechenweg an. x + 3 passt immer, egal wie viele Bücher Arne hat.
x ist eine Variable.
Für Variablen kannst du Zahlen einsetzen und dann das Ergebnis ausrechnen.
Schrittfolge für das Aufstellen von Termen
Beispiel 1: Jan, Aziz und Marleen wollen eine Fahrradtour zur Nordsee machen. Wie weit müssen sie täglich fahren, wenn sie die Strecke von 240 km auf verschieden viele Tage aufteilen?
Stelle einen Term auf.
1. Schritt: Wie würdest du bei Zahlen vorgehen? Schreibe den Rechenweg für mehrere Beispiele auf.
Wähle verschiedene Anzahlen von Tagen und berechne.
| Gesamtstrecke | Anzahl der Tage | Du rechnest |
|---|---|---|
| 240 | 10 | 240:10 |
| 240 | 8 | 240:8 |
| 240 | 5 | 240:5 |

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Schrittfolge für das Aufstellen von Termen
2. Schritt: Was ändert sich? Was bleibt gleich?
| Gesamtstrecke | Anzahl der Tage | Du rechnest |
|---|---|---|
| 240 | 10 | 240:10 |
| 240 | 8 | 240:8 |
| 240 | 5 | 240:5 |
In der Tabelle siehst du:
- Die Gesamtstrecke bleibt gleich.
- Die Anzahl der Tage ändert sich. → Das wird deine Variable x.
3. Schritt: Schreibe die Rechnung in einem Term mit Variablen auf.
Der Term für die Aufgabe ist 240:x
Mathematiker nutzen für Variablen meistens den Buchstaben x.
Du kannst aber auch andere Buchstaben benutzen, wie y, z oder a und b.
Die Sprache der Mathematik
In der Umgangssprache benutzt du Wörter wie hinzu oder das Doppelte oder ausgeben.
Diese Wörter übersetzt du in die Sprache der Mathematik.
Beispiele:
| hinzu | + (plus rechnen) |
| das Doppelte | ⋅2 |
| ausgeben | - (minus rechnen) |
Mithilfe dieser Wörter weißt du, wie du den Term aufstellst.
Häufige mathematische Begriffe:
| doppelt, dreifach, vierfach | ⋅2, ⋅3, ⋅4 |
| Hälfte, dritter Teil, vierter Tei | :2, :3, :4 |
| vermehrt um 2 | +2 |
| verringert um 2 | -2 |
Einen längeren Term aufstellen
Beispiel 2: Marko kauft für seine Geburtstagsfeier mehrere Flaschen Limonade und eine Riesentafel Schokolade. Jede Flasche kostet 1,25 €. Die Schokolade kostet 3 €.
Wie viel muss Marko bezahlen?
Stelle einen Term auf.
1. Schritt: Wie würdest du bei Zahlen vorgehen? Schreibe den Rechenweg für mehrere Beispiele auf.
Wähle verschiedene Anzahlen von Flaschen und berechne.
| Preis Flasche | Anzahl der Flaschen | Preis Schokolade | Du rechnest |
|---|---|---|---|
| 1,25 | 6 | 3 | 1,25⋅6+3 |
| 1,25 | 12 | 3 | 1,25⋅12+3 |
| 1,25 | 8 | 3 | 1,25⋅8+3 |

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
Einen längeren Term aufstellen
2. Schritt: Was ändert sich? Was bleibt gleich?
| Preis Flasche | Anzahl der Flaschen | Preis Schokolade | Du rechnest |
|---|---|---|---|
| 1,25 | 6 | 3 | 1,25⋅6+3 |
| 1,25 | 12 | 3 | 1,25⋅12+3 |
| 1,25 | 8 | 3 | 1,25⋅8+3 |
In der Tabelle siehst du:
- Der Preis pro Flasche bleibt gleich.
- Der Preis für die Schokolade bleibt gleich.
- Die Anzahl der Flaschen ändert sich. → Das wird deine Variable x
3. Schritt: Schreibe die Rechnung in einem Term mit Variablen auf.
Der Term für die Aufgabe ist 1,25⋅x+3
So stellst du einen Term auf
1. Schritt: Wie würdest du bei Zahlen vorgehen? Schreibe den Rechenweg für mehrere Beispiele auf.
2. Schritt: Was ändert sich? Was bleibt gleich?
3. Schritt: Schreibe die Rechnung in einem Term mit Variablen auf.
Terme mit dem Formel-Editor
So gibst du Terme auf kapiert.de ein:

Noch nicht kapiert?
kapiert.dekann mehr:
- interaktive Übungen
und Tests - individueller Klassenarbeitstrainer
- Lernmanager
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen