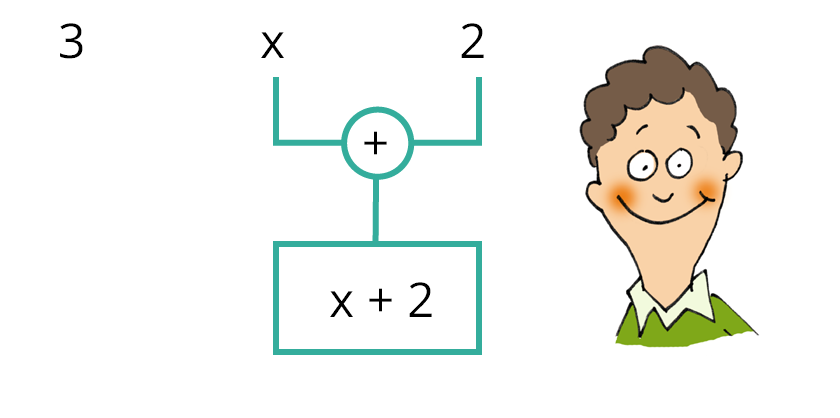Terme mit einer Variablen zusammenfassen
Terme mit 2 gleichen Gliedern zusammenfassen
Oft kannst du Terme zusammenfassen. So sparst du Schreib- und Rechenarbeit.
Beispiel: 2x+3x
Die Glieder 2x und 3x sind gleichartig (oder gleich), weil in beiden die gleiche Variable x vorkommt. Die Vorfaktoren 2 und 3 können sich unterscheiden.
Addiere die Vorfaktoren:
2x+3x=5x
↓ ↓ ↑
2 + 3 =5
Das Distributivgesetz besagt:
2·4+3·4
=(2+3)·4
Das gilt natürlich auch, wenn man anstatt der 4 eine Variable x benutzt.
2·x+3·x
=(2+3)·x
=5·x
Terme mit 2 gleichen Gliedern zusammenfassen
Lange Terme kannst du oft zusammenfassen. Dafür sind die Vorzeichen vor den Termgliedern wichtig.
Beispiel: x-2x
Das Minus in -2x gehört zum Vorfaktor. Der Vorfaktor ist also -2.
Berechne die Vorfaktoren:
x-2x=-x
↓ ↓ ↑
1 - 2 =-1
Du addierst oder subtrahierst gleichartige Terme, indem du die Vorfaktoren addierst oder subtrahierst.
Der Vorfaktor von x ist 1.
Einsen werden meist weggelassen:
1·x=x.
Der Vorfaktor -1 wird nur zu „-“, denn
-1·x=-x.
Terme mit verschiedenen Gliedern zusammenfassen
Termglieder müssen nicht immer gleich sein.
Beispiel: 3x-x+5+1
- Die Glieder 3x und -x sind gleich, denn sie beinhalten die gleiche Variable.
- Die Glieder 5 und 1 haben keine Variable.
Du kannst die Glieder, die gleich sind, zusammenfassen.
3x−x+5+1=2x + 6
↓ ↓
5+1=
↑
6
= 2
Du kannst nur gleichartige Glieder in einem Term zusammenfassen!
Glieder, die keine Variable beinhalten sind auch gleich!
Mit dem Distributivgesetz:
3x-x+5+1
=(3-1)·x+(5+1)
=2·x+6
TESTEN
=2
3x-x+5+1=2x+6
↓ ↓ ↓ ↓ ↑ ↑
5+1= 6
3 - 1 =2
3x-x+5+1=2x+6
↓ ↓ ↓ ↓ ↑ ↑
↓ ↓ 5+1= ↑ 6
3 - 1 =2
3x-x+5+1=2x+6
↓ ↓ ↑
↓ ↓ 5+1= ↑ 6
3 - 1 =2
| 3x-x + 5+1 = 2x + 6 | |||
| ↓ ↓ | ↓ ↓ | ↑ | ↑ |
| 5+1 = | 6 | ||
| 3 - 1 | = | 2 | |
Achtung, Vorzeichen!
Terme können aus vielen Termgliedern bestehen.
5x+4-2x-3-x
Die Glieder 5x, -2x und -x sind gleich und die Glieder +4 und -3 sind gleich.
Zuerst sortierst du die Terme. Dabei ist ganz wichtig, dass du immer die Vorzeichen + und - „mit nimmst“.
5x-2x-x+4-3
Dann fasst du die Termglieder zusammen.
5x-2x-x+4-3=2x+1
4-3= 1
5 -2 -1 =2
Du erhältst einen viel kürzeren und einfacheren Term.
Vorzeichen gehören zu dem darauf folgenden Termglied. Nach dem Sortieren steht vor jedem Termglied dasselbe Zeichen (+ oder -) wie vor dem Sortieren.
Mit dem Distributivgesetz:
5x-2x-x+4-3
=(5-2-1)·x+(4-3)
=2·x+1
Terme mit Brüchen zusammenfassen
Vorfaktoren müssen nicht immer natürliche oder ganze Zahlen sein.
12x+13-34x+114x+23
Auch hier sortierst du zuerst.
12x-34x+114x+13+23
Und nun fasst du gleiche Termglieder zusammen.
12x-34x+114x+13+23 = x+1
12 -34 +114 =1
13+23= 1
Achtung: Wieder die Vorzeichen mitnehmen!
12x, -34x und 114x sind gleichartige Glieder.
13 und 23 sind gleichartige Glieder.
Terme mit anderen Variablen
Die Variable heißt nicht immer x.
3y+2-y+1
Dennoch gehst du genauso vor.
Sortieren:
3y-y+2+1
Zusammenfassen:
3y-y+2+1=2y+3
3 -1 =2
2+1 = 3
So fasst du Terme zusammen:
- Sortiere gleichartige Termglieder.
- Glieder mit Variable
- Zahlen
Dabei nimmst du immer das Vorzeichen mit.
2. Fasse die gleichen Termglieder zusammen, indem du
- die Vorfaktoren der Variablen addierst oder subtrahierst
- die Zahlen addierst oder subtrahierst
Terme mit dem Formel-Editor
So gibst du Terme auf kapiert.de ein:
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen